题目内容
8.下列说法正确的有( )个.①分数都是有理数;②无限小数都是无理数;③任何数的平方根都是无理数;④无理数与无理数的和一定是无理数.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 无限不循环小数是无理数,有理数是指有限小数和无限循环小数,包括整数和分数,由此可判断选项的正确性.
解答 解:①分数都是有理数,正确;
②因为无限不循环小数是无理数,所以无限小数都是无理数,错误;
③任何数的平方根都是无理数,错误,例如,1的平方根是±1;
④无理数与无理数的和一定是无理数,错误,例如,$\sqrt{2}+(-\sqrt{2})=0$;
故选A.
点评 本题考查了对无理数和有理数,注意:有理数是指有限小数和无限循环小数,包括整数和分数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16. 如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )
如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )
 如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )
如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )| A. | 43° | B. | 47° | C. | 120° | D. | 133° |
20.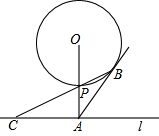 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )
 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )| A. | $\frac{5}{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\frac{5\sqrt{3}}{3}$ |
17.在一个已经装有10个黑色玻璃球的不透明布袋中再装入30个红色、白色玻璃球,这些球除颜色外其他完全相同.小花做摸球实验,她将袋子里面的球充分搅均匀后从中随机摸出一个球记下颜色,再把它放回袋子里,不断重复上述过程,下表是实验中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P白=0.6;
(3)从中选出12个玻璃球设计摸球游戏,使摸到红球的概率和摸到白球的概率相等.
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 67 | 122 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.67 | 0.61 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)假如你摸一次,你摸到白球的概率P白=0.6;
(3)从中选出12个玻璃球设计摸球游戏,使摸到红球的概率和摸到白球的概率相等.
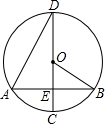 如图,在⊙O中,弦AB垂直于直径CD,垂足为E,连接OB、AD,∠ADC=30°,弦AB=2$\sqrt{3}$.
如图,在⊙O中,弦AB垂直于直径CD,垂足为E,连接OB、AD,∠ADC=30°,弦AB=2$\sqrt{3}$.