题目内容
11.在Rt△ABC中,∠C=90°,∠A=25°,则∠B的度数为65°.分析 根据直角三角形两锐角互余可得∠A+∠B=90°,再代入∠A的度数可得答案.
解答 解:∵在Rt△ABC中,∠C=90°,
∴∠A+∠B=90°,
∵∠A=25°,
∴∠B=90°-25°=65°,
故答案为:65°.
点评 此题主要考查了直角三角形的性质,关键是掌握在直角三角形中,两个锐角互余.

练习册系列答案
相关题目
1.等腰直角三角形的斜边长为a,则其斜边上的高为( )
| A. | $\frac{a}{2}$ | B. | $\sqrt{2}a$ | C. | $\frac{\sqrt{3}}{2}$a | D. | $\frac{\sqrt{2}}{4}$a |
16. 如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )
如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )
 如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )
如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )| A. | 43° | B. | 47° | C. | 120° | D. | 133° |
20.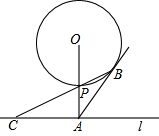 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )
 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )| A. | $\frac{5}{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\frac{5\sqrt{3}}{3}$ |
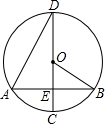 如图,在⊙O中,弦AB垂直于直径CD,垂足为E,连接OB、AD,∠ADC=30°,弦AB=2$\sqrt{3}$.
如图,在⊙O中,弦AB垂直于直径CD,垂足为E,连接OB、AD,∠ADC=30°,弦AB=2$\sqrt{3}$.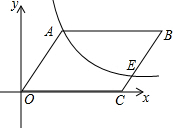 如图,平行四边形OABC中,OC=6,点P(4,8)在直线OA上,点E在BC上,BE=2CE,反比例函数y=$\frac{k}{x}$的图象经过A、E的两点,则k=$\frac{81}{8}$.
如图,平行四边形OABC中,OC=6,点P(4,8)在直线OA上,点E在BC上,BE=2CE,反比例函数y=$\frac{k}{x}$的图象经过A、E的两点,则k=$\frac{81}{8}$.