题目内容
9.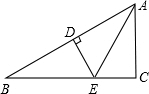 如图,AB的垂直平分线交AB于D,交BC于E,AE平分∠BAC,∠B=30°,DE=2cm,则BC的长是( )
如图,AB的垂直平分线交AB于D,交BC于E,AE平分∠BAC,∠B=30°,DE=2cm,则BC的长是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
分析 根据角平分线上的点到角的两边距离相等可得CE=DE,根据直角三角形30°角所对的直角边等于斜边的一半可得BE=2DE,然后根据BC=BE+CE代入数据计算即可得解.
解答 解:∵AE平分∠BAC,DE⊥AB,∠C=90°,
∴CE=DE=2cm,
∵∠B=30°,
∴BE=2DE=2×2=4cm,
∴BC=BE+CE=4+2=6cm.
故选D.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
20.25的平方根是( )
| A. | ±5 | B. | -5 | C. | 5 | D. | 25 |
17.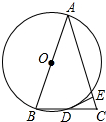 如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.
如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.
(1)求证:DE为⊙O的切线;
(2)若AB=13,sinB=$\frac{12}{13}$,求CE的长.
 如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.
如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.(1)求证:DE为⊙O的切线;
(2)若AB=13,sinB=$\frac{12}{13}$,求CE的长.
1.等腰直角三角形的斜边长为a,则其斜边上的高为( )
| A. | $\frac{a}{2}$ | B. | $\sqrt{2}a$ | C. | $\frac{\sqrt{3}}{2}$a | D. | $\frac{\sqrt{2}}{4}$a |
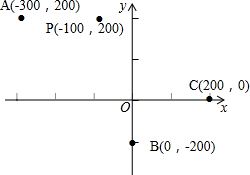 某地震多发地区有互相垂直的两条交通主干线,以这两条主干线为轴建立直角坐标系,1个单位长度为100km,地震监测部门测得该地区发生过一次地震,震中位置为P(-100,200),影响范围的半径为300km,如图所示,主干线沿线附近有3个城市:A(-300,200),B(0,-100),C(200,0),问在地震中受影响的是哪些城市?为什么?
某地震多发地区有互相垂直的两条交通主干线,以这两条主干线为轴建立直角坐标系,1个单位长度为100km,地震监测部门测得该地区发生过一次地震,震中位置为P(-100,200),影响范围的半径为300km,如图所示,主干线沿线附近有3个城市:A(-300,200),B(0,-100),C(200,0),问在地震中受影响的是哪些城市?为什么?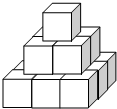 如图把14个棱长为1分米的正方体摆放在课桌上,现在想露出的表面都涂上颜色,则涂上颜色部分的面积为33平方分米.
如图把14个棱长为1分米的正方体摆放在课桌上,现在想露出的表面都涂上颜色,则涂上颜色部分的面积为33平方分米.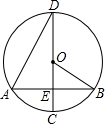 如图,在⊙O中,弦AB垂直于直径CD,垂足为E,连接OB、AD,∠ADC=30°,弦AB=2$\sqrt{3}$.
如图,在⊙O中,弦AB垂直于直径CD,垂足为E,连接OB、AD,∠ADC=30°,弦AB=2$\sqrt{3}$.