题目内容
9.使代数式$\sqrt{x-2015}$有意义的x的取值范围是x≥2015.分析 根据二次根式的被开方数是非负数,可得答案.
解答 解:使代数式$\sqrt{x-2015}$有意义,得
x-2015≥0.解得x≥2015,
故答案为:x≥2015.
点评 本题考查了二次根式有意义的条件,二次根式中的被开方数必须是非负数,否则二次根式无意义.

练习册系列答案
相关题目
20.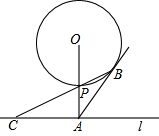 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )
 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )| A. | $\frac{5}{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\frac{5\sqrt{3}}{3}$ |
17.在一个已经装有10个黑色玻璃球的不透明布袋中再装入30个红色、白色玻璃球,这些球除颜色外其他完全相同.小花做摸球实验,她将袋子里面的球充分搅均匀后从中随机摸出一个球记下颜色,再把它放回袋子里,不断重复上述过程,下表是实验中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P白=0.6;
(3)从中选出12个玻璃球设计摸球游戏,使摸到红球的概率和摸到白球的概率相等.
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 67 | 122 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.67 | 0.61 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)假如你摸一次,你摸到白球的概率P白=0.6;
(3)从中选出12个玻璃球设计摸球游戏,使摸到红球的概率和摸到白球的概率相等.
19.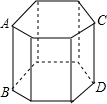 如图,直六棱柱的底面是边长为4cm的正六边形,AB为8cm,则此直六棱柱左视图的面积为( )
如图,直六棱柱的底面是边长为4cm的正六边形,AB为8cm,则此直六棱柱左视图的面积为( )
 如图,直六棱柱的底面是边长为4cm的正六边形,AB为8cm,则此直六棱柱左视图的面积为( )
如图,直六棱柱的底面是边长为4cm的正六边形,AB为8cm,则此直六棱柱左视图的面积为( )| A. | 32$\sqrt{3}$cm2 | B. | 32cm2 | C. | 64cm2 | D. | 16$\sqrt{3}$cm2 |
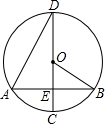 如图,在⊙O中,弦AB垂直于直径CD,垂足为E,连接OB、AD,∠ADC=30°,弦AB=2$\sqrt{3}$.
如图,在⊙O中,弦AB垂直于直径CD,垂足为E,连接OB、AD,∠ADC=30°,弦AB=2$\sqrt{3}$.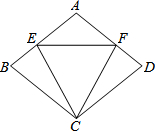 如图,等腰△CEF的两腰CE、CF的长与菱形ABCD的边长相等.
如图,等腰△CEF的两腰CE、CF的长与菱形ABCD的边长相等.