题目内容
16.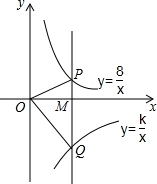 如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数y=$\frac{8}{x}$(x>0)和y=$\frac{k}{x}$(x>0)的图象交于P、Q两点,若S△POQ=13,则k的值为-18.
如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数y=$\frac{8}{x}$(x>0)和y=$\frac{k}{x}$(x>0)的图象交于P、Q两点,若S△POQ=13,则k的值为-18.
分析 根据反比例函数系数k的几何意义,则△OPM和△OMQ的面积都可求得(或用k表示),根据△POQ的面积,即可得到一个关于k的方程,进而求解.
解答 解:S△OPM=$\frac{1}{2}$×8=4,
S△OMQ=$\frac{1}{2}$|k|=-$\frac{1}{2}$k,
∵S△POQ=13,
∴4-$\frac{1}{2}$k=13,
解得:k=-18.
故答案是:-18.
点评 本题考查了反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.本知识点是中考的重要考点,同学们应高度关注.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
11.当-1≤x≤1时,在实数范围内下列式子有意义的是( )
| A. | $\sqrt{(x+1)(x-1)}$ | B. | $\sqrt{(x+1)(1-x)}$ | C. | $\sqrt{\frac{x+1}{x-1}}$ | D. | $\sqrt{\frac{x-1}{x+1}}$ |
1.下列说法正确的是( )
| A. | 面积相等的两个三角形是全等三角形 | |
| B. | 周长相等的两个三角形是全等三角形 | |
| C. | 有两条边和一个角对应相等的两个三角形是全等三角形 | |
| D. | 两角和其中一个角的对边分别相等的两个三角形是全等三角形 |
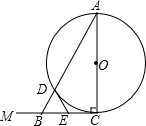 如图1,已知∠ACM=90°,且AC=2,以AC为直径作⊙O,B是射线CM上的一动点,以1个单位/秒,从点C向CM方向运动,运动时间为t秒,连结AB交⊙O 于另一点D,BC的中点为E,
如图1,已知∠ACM=90°,且AC=2,以AC为直径作⊙O,B是射线CM上的一动点,以1个单位/秒,从点C向CM方向运动,运动时间为t秒,连结AB交⊙O 于另一点D,BC的中点为E,