题目内容
18.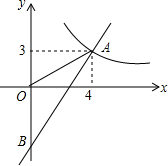 如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.(1)求函数y=kx+b和y=$\frac{a}{x}$的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
分析 (1)利用待定系数法即可解答;
(2)设点M的坐标为(x,2x-5),根据MB=MC,得到$\sqrt{{x}^{2}+(2x-5+5)^{2}}=\sqrt{{x}^{2}+(2x-5-5)^{2}}$,即可解答.
解答 解:(1)把点A(4,3)代入函数y=$\frac{a}{x}$得:a=3×4=12,
∴y=$\frac{12}{x}$.
OA=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵OA=OB,
∴OB=5,
∴点B的坐标为(0,-5),
把B(0,-5),A(4,3)代入y=kx+b得:
$\left\{\begin{array}{l}{b=-5}\\{4k+b=3}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=2}\\{b=-5}\end{array}\right.$
∴y=2x-5.
(2)∵点M在一次函数y=2x-5上,
∴设点M的坐标为(x,2x-5),
∵MB=MC,
∴$\sqrt{{x}^{2}+(2x-5+5)^{2}}=\sqrt{{x}^{2}+(2x-5-5)^{2}}$
解得:x=2.5,
∴点M的坐标为(2.5,0).
点评 本题考查了一次函数与反比例函数的交点,解决本题的关键是利用待定系数法求解析式.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
8.甲箱内有4颗球,颜色分别为红、黄、绿、蓝;乙箱内有3颗球,颜色分别为红、黄、黑.小赖打算同时从甲、乙两个箱子中各抽出一颗球,若同一箱中每球被抽出的机会相等,则小赖抽出的两颗球颜色相同的机率为何?( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{7}$ | D. | $\frac{7}{12}$ |
9.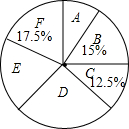 某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
根据图表提供的信息,下列结论错误的是( )
 某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)| 选修课 | A | B | C | D | E | F |
| 人数 | 40 | 60 | 100 |
| A. | 这次被调查的学生人数为400人 | |
| B. | 扇形统计图中E部分扇形的圆心角为72° | |
| C. | 被调查的学生中喜欢选修课E、F的人数分别为80,70 | |
| D. | 喜欢选修课C的人数最少 |
6. 如图,l1∥l2,∠1=56°,则∠2的度数为( )
如图,l1∥l2,∠1=56°,则∠2的度数为( )
 如图,l1∥l2,∠1=56°,则∠2的度数为( )
如图,l1∥l2,∠1=56°,则∠2的度数为( )| A. | 34° | B. | 56° | C. | 124° | D. | 146° |
3.已知一个正多边形的内角是140°,则这个正多边形的边数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
7.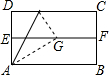 如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
 如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
8.地球与月球的平均距离为384 000km,将384 000这个数用科学记数法表示为( )
| A. | 3.84×103 | B. | 3.84×104 | C. | 3.84×105 | D. | 3.84×106 |
 如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=24,AH=18,⊙O的半径OC=13,则AB=$\frac{39}{2}$.
如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=24,AH=18,⊙O的半径OC=13,则AB=$\frac{39}{2}$.