题目内容
8.甲箱内有4颗球,颜色分别为红、黄、绿、蓝;乙箱内有3颗球,颜色分别为红、黄、黑.小赖打算同时从甲、乙两个箱子中各抽出一颗球,若同一箱中每球被抽出的机会相等,则小赖抽出的两颗球颜色相同的机率为何?( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{7}$ | D. | $\frac{7}{12}$ |
分析 画出树状图,得出共有12种等可能的结果,颜色相同的有2种情形,即可得出结果.
解答 解:树状图如图所示:
共有12种等可能的结果,颜色相同的有2种情形,
故小赖抽出的两颗球颜色相同的机率=$\frac{2}{12}$=$\frac{1}{6}$;
故选:B.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.小明、小亮同时为校园文化艺术节制作彩旗,已知小明每小时比小亮多做5面彩旗,小明做60面彩旗与小亮做50面彩旗所用时间相同,问小明每小时做多少面彩旗?若设小明每小时做x面彩旗,则下列方程组符合题意的是( )
| A. | $\frac{60}{x}$=$\frac{50}{x-5}$ | B. | $\frac{50}{x}$=$\frac{60}{x-5}$ | C. | $\frac{60}{x}$=$\frac{50}{x+5}$ | D. | $\frac{50}{x}$=$\frac{60}{x+5}$ |
16.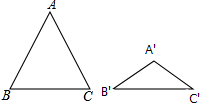 如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为( )
如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为( )
 如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为( )
如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为( )| A. | 25:9 | B. | 5:3 | C. | $\sqrt{5}$:$\sqrt{3}$ | D. | 5$\sqrt{5}$:3$\sqrt{3}$ |
13.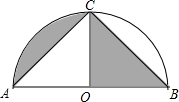 如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是( )
如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是( )
 如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是( )
如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是( )| A. | $\frac{π}{4}$ | B. | $\frac{1}{2}$$+\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{1}{2}$+$\frac{π}{2}$ |
17. 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )
 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
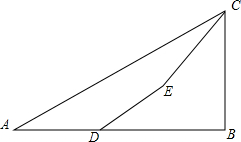 如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取$\sqrt{3}$=1.732,结果精确到0.1m).
如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取$\sqrt{3}$=1.732,结果精确到0.1m). 如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.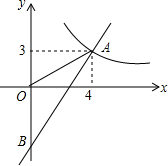 如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.