题目内容
16.若圆锥的高是8cm,母线长10cm,则其全面积=96πcm2.分析 利用勾股定理可得圆锥的底面半径,圆锥的全面积=π×底面半径×母线长+π×半径2,把相关数值代入即可求解.
解答 解:∵圆锥的高为8cm,母线长为10cm,
∴圆锥的底面半径为6cm,
∴圆锥的全面积为π×6×10+π×62=96πcm2.
故答案为:96πcm2
点评 考查圆锥的全面积计算公式;用到的知识点为:圆锥的底面半径,母线长,高组成直角三角形,可利用勾股定理求解.

练习册系列答案
相关题目
7. 如图,∠3+∠4=180°,∠2=135°,则∠1度数是( )
如图,∠3+∠4=180°,∠2=135°,则∠1度数是( )
 如图,∠3+∠4=180°,∠2=135°,则∠1度数是( )
如图,∠3+∠4=180°,∠2=135°,则∠1度数是( )| A. | 45° | B. | 55° | C. | 65° | D. | 75° |
11.已知两条线段长分别为3、4,那么能与它们组成直角三角形的第三条线段长是( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 不能确定 |
5.已知P1(x1,y1),P2(x2,y2),P(x3,y3)是反比例函数$y=\frac{k^2}{x}$(k≠0)的图象上的三点,且x1<x2<0<x3,则y1,y2,y3的大小关系是( )
| A. | y3<y2<y1 | B. | y2<y1<y3 | C. | y1<y2<y3 | D. | y2<y3<y1 |
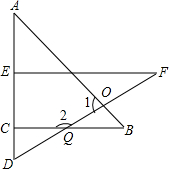 一副三角板的两个三角形ABC与DEF的拼图如图所示,A、E、C、D在同一直线上,其中∠A=45°,∠F=30°
一副三角板的两个三角形ABC与DEF的拼图如图所示,A、E、C、D在同一直线上,其中∠A=45°,∠F=30° 如图,在长为4x+3,宽为3x+5的长方形纸片中剪去两个边长分别为-2x+1,x+2的正方形,求阴影部分的面积.
如图,在长为4x+3,宽为3x+5的长方形纸片中剪去两个边长分别为-2x+1,x+2的正方形,求阴影部分的面积. 如图有A、B两个大小均匀的转盘,其中A转盘被分成3等份,B转盘被分成4等份,并在每一份内标上数字.同时转动两个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A转盘指针指向的数字记作m,将B转盘指针指向的数字记作n.
如图有A、B两个大小均匀的转盘,其中A转盘被分成3等份,B转盘被分成4等份,并在每一份内标上数字.同时转动两个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A转盘指针指向的数字记作m,将B转盘指针指向的数字记作n.