题目内容
6.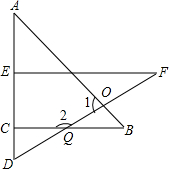 一副三角板的两个三角形ABC与DEF的拼图如图所示,A、E、C、D在同一直线上,其中∠A=45°,∠F=30°
一副三角板的两个三角形ABC与DEF的拼图如图所示,A、E、C、D在同一直线上,其中∠A=45°,∠F=30°(1)求证:EF∥BC;
(2)求∠1、∠2的度数.
分析 (1)由垂直于同一条直线的两直线平行,可证EF∥BC.
(2)由三角形的一个外角等于与它不相邻的两个内角的和可求∠1与∠2的度数.
解答 解:(1)∵EF⊥AD,BC⊥AD,
∴BC∥EF(同一平面内,垂直于同一条直线的两直线平行).
(2)∵∠APE=180°-∠AEP-∠A=180°-90°-45°=45°,
又∵∠APE=∠OPF,
∴∠1=∠F+∠OPF=30°+45°=75°,
∠2=∠DCQ+∠D=90°+60°=150°.
点评 本题考查平行线的判定与性质,涉及到三角形外角的性质及三角形的内角和定理,解答的关键是沟通外角和内角的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.对于同一平面内的三条直线a,b,c,下列命题中不正确的是( )
| A. | 若a∥b,b∥c,则a∥c | B. | 若a⊥b,a⊥c,则b⊥c | C. | 若a∥b,a⊥c,则b⊥c | D. | 若a⊥b,a⊥c,则b∥c |
14.已知四边形ABCD是平行四边形,下列结论不正确的是( )
| A. | 当AC=BD时,它是菱形 | B. | 当AC⊥BD时,它是菱形 | ||
| C. | 当∠ABC=90°时,它是矩形 | D. | 当AB=BC时,它是菱形 |
18.计算(-6)÷(-2)的结果是( )
| A. | 3 | B. | -3 | C. | 4 | D. | -4 |