题目内容
5.已知P1(x1,y1),P2(x2,y2),P(x3,y3)是反比例函数$y=\frac{k^2}{x}$(k≠0)的图象上的三点,且x1<x2<0<x3,则y1,y2,y3的大小关系是( )| A. | y3<y2<y1 | B. | y2<y1<y3 | C. | y1<y2<y3 | D. | y2<y3<y1 |
分析 先根据反比例函数$y=\frac{k^2}{x}$(k≠0)的系数k2>0判断出函数图象在一、三象限,在每个象限内,y随x的增大而减小,再根据x1<x2<0<x3,判断出y1、y2、y3的大小.
解答 解:∵k2>0,函数图象如图,则图象在第一、三象限,在每个象限内,y随x的增大而减小,
又∵x1<x2<0<x3,
∴P1(x1,y1),P2(x2,y2)在第三象限,P(x3,y3)在第一象限,
∴y2<y1<0,y3>0
∴y2<y1<y3.
故选B.
点评 本题考查了由反比例函数的图象和性质确定y2,y1,y3的关系.注意是在每个象限内,y随x的增大而减小.不能直接根据x的大小关系确定y的大小关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
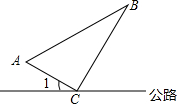 如图,在公路的同侧有A、B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5km/h,问多长时间后这人距离B送奶站最近?
如图,在公路的同侧有A、B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5km/h,问多长时间后这人距离B送奶站最近? 如图所示,请将图中的“蘑菇”向左平移6个格,再向下平移2个格.
如图所示,请将图中的“蘑菇”向左平移6个格,再向下平移2个格.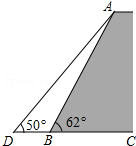 如图,一堤坝的坡角∠ABC=62°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到1米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
如图,一堤坝的坡角∠ABC=62°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到1米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)