Question

18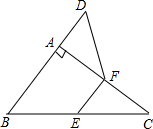．如图，在△ABC中，∠BAC=90°，延长BA到点D，使AD=$\frac{1}{2}$AB，E，F分别是边BC，AC的中点，试猜想DF与EC的数量关系，并证明你的猜想．

Answer 1

分析 由直角三角形的性质和三角形中位线定理得出AE=$\frac{1}{2}$BC=EC，EF∥AB，EF=$\frac{1}{2}$AB，得出AD∥EF，AD=EF，证出四边形AEFD是平行四边形，得出AE=DF，即可得出结论．

解答 解：DF=EC；理由如下：
连接AE，如图所示：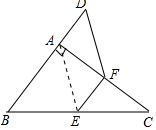
∵∠BAC=90°，E，F分别是边BC，AC的中点，
∴AE=$\frac{1}{2}$BC=EC，EF∥AB，EF=$\frac{1}{2}$AB，
∵AD=$\frac{1}{2}$AB，
∴AD∥EF，AD=EF，
∴四边形AEFD是平行四边形，
∴AE=DF，
∴DF=EC．

点评 本题考查了三角形中位线定理、直角三角形斜边上的中线性质、平行四边形的判定与性质；熟练掌握三角形中位线定理，证明四边形是平行四边形是解决问题的关键．