题目内容
9.如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF,将纸片ACB的一角沿EF折叠.(1)如图①,若折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△AEF,则AE=$\frac{5}{2}$;
(2)如图②,若折叠后点A落在BC边上的点M处,且使MF∥CA.求AE的长;
(3)如图③,若折叠后点A落在BC延长线上的点N处,且使NF⊥AB.求AE的长.

分析 (1)由折叠的性质得出EF⊥AB,△AEF≌△DEF,得出S△AEF≌S△DEF,由已知得出S△ABC=4S△AEF,证明△AEF∽△ABC,得出$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=($\frac{AE}{AB}$)2,即可求出AE的长;
(2)设AE=x,则CE=4-x.由折叠可知:AE=EM=x,AF=MF,∠AFE=∠MFE,证明四边形AEMF为菱形.得出EM∥AB.由平行线证明△CME∽△CBA.得出对应边成比例,即可得出AE的长;
(3)设AE=y,则CE=4-y.由折叠可知:AE=EN=y,AF=NF,证明△NBF∽ABC.得出对应边成比例求出BF=$\frac{3}{4}$NF=$\frac{3}{4}$AF.由BF+AF=AB=5得出方程,解方程得出BF=$\frac{15}{7}$,NF=$\frac{20}{7}$,由勾股定理求出BN=$\sqrt{B{F}^{2}+N{F}^{2}}$=$\frac{25}{7}$,得出CN=BN-BC=$\frac{4}{7}$.在Rt△CEN中,由勾股定理得出方程,解方程即可.
解答 解:(1)∵△ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,
∴EF⊥AB,△AEF≌△DEF,
∴S△AEF≌S△DEF,
∵S四边形ECBF=3S△EDF,
∴S△ABC=4S△AEF,
在Rt△ABC中,∵∠ACB=90°,AC=4,BC=3,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵∠EAF=∠BAC,
∴△AEF∽△ABC,
∴$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=($\frac{AE}{AB}$)2,即($\frac{AE}{5}$)2=$\frac{1}{4}$,
∴AE=$\frac{5}{2}$;
故答案为:$\frac{5}{2}$;
(2)设AE=x,则CE=4-x.
由折叠可知:AE=EM=x,AF=MF,∠AFE=∠MFE,
∵MF∥AC,
∴∠AEF=∠MFE.
∴∠AEF=∠AFE.
∴AE=AF.
∴AE=EM=MF=AF,
∴四边形AEMF为菱形.
∴EM∥AB.∴△CME∽△CBA.
∴$\frac{CE}{CA}$=$\frac{EM}{AB}$,即$\frac{4-x}{4}$=$\frac{x}{5}$,解得x=$\frac{20}{9}$,即AE=$\frac{20}{9}$;
(3)设AE=y,则CE=4-y.
由折叠可知:AE=EN=y,AF=NF,
∵NF⊥AB,
∴∠NFB=90°.
∵∠ACB=90°,
∴∠NFB=∠ACB.
且∠NBF=∠ABC,
∴△NBF∽ABC.
∴$\frac{BF}{NF}$=$\frac{BC}{AC}$=$\frac{3}{4}$.即BF=$\frac{3}{4}$NF=$\frac{3}{4}$AF.由BF+AF=AB=5,
解得:BF=$\frac{15}{7}$,NF=$\frac{20}{7}$,
∴BN=$\sqrt{B{F}^{2}+N{F}^{2}}$=$\frac{25}{7}$,
∴CN=BN-BC=$\frac{25}{7}$-3=$\frac{4}{7}$.
在Rt△CEN中,由勾股定理得:CN2+CE2=EN2,
∴($\frac{4}{7}$)2+(4-y)2=y2,
解得:y=$\frac{100}{49}$,
即AE=$\frac{100}{49}$.
点评 本题是四边形综合题,考查了折叠的性质、相似三角形的判定和性质、勾股定理、菱形的判定和性质等知识;本题综合性强,有一定难度,证明三角形相似和运用勾股定理得出方程是解决问题的关键,属于中考常考题型.

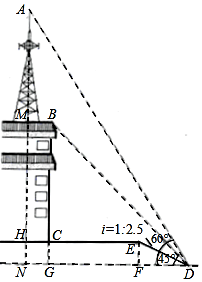 如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73供选用,结果保留整数)
如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73供选用,结果保留整数) 如图,是一个几何体的三视图,由图中数据计算此几何体的表面积为28π(结果保留π).
如图,是一个几何体的三视图,由图中数据计算此几何体的表面积为28π(结果保留π).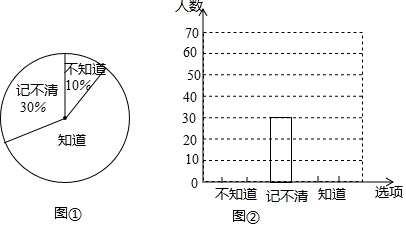
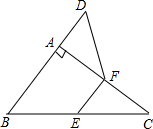 如图,在△ABC中,∠BAC=90°,延长BA到点D,使AD=$\frac{1}{2}$AB,E,F分别是边BC,AC的中点,试猜想DF与EC的数量关系,并证明你的猜想.
如图,在△ABC中,∠BAC=90°,延长BA到点D,使AD=$\frac{1}{2}$AB,E,F分别是边BC,AC的中点,试猜想DF与EC的数量关系,并证明你的猜想. 如图,在正方形ABCD中,AB=6,分别以A、B、C、D为圆心,以正方形的边长为半径画弧,弧的交点设为E,F,G,H,则图中阴影部分的面积是$\frac{3+π-3\sqrt{3}}{3}$a2.
如图,在正方形ABCD中,AB=6,分别以A、B、C、D为圆心,以正方形的边长为半径画弧,弧的交点设为E,F,G,H,则图中阴影部分的面积是$\frac{3+π-3\sqrt{3}}{3}$a2.