题目内容
20.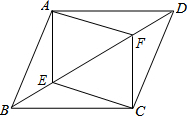 如图,在四边形ABCD中,点E,F是对角线BD上的两点,且BE=DF.
如图,在四边形ABCD中,点E,F是对角线BD上的两点,且BE=DF.(1)如果四边形AECF是平行四边形,求证:四边形ABCD也是平行四边形;
(2)如果四边形AECF是菱形,求证:四边形ABCD也是菱形.
分析 (1)只要证明OA=OC,OB=OD即可解决问题.
(2)只要证明四边形ABCD是平行四边形,再证明AC⊥BD即可证明.
解答 证明:(1)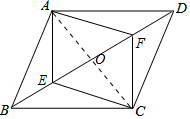 连接AC交BD于O.
连接AC交BD于O.
∵四边形AECF是平行四边形,
∴OA=OC,OE=OF,
∵BE=DF,
∴OB=OD,∵OA=OC,
∴四边形ABCD是平行四边形.
(2)连接AC交BD于O.
∵四边形AECF是菱形,
∴OA=OC,OE=OF,AC⊥EF,
∵BE=DF,
∴OB=OD,∵OA=OC,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形.
点评 本题考查平行四边形的性质和判定、菱形的性质和判定等知识,解题的关键是熟练掌握平行四边形的性质和判定,菱形的性质和判定,属于中考常考题型.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
12.直线y=x+3上有一点P(3,n),则点P关于原点的对称点P′的坐标是( )
| A. | (-3,-6) | B. | (-6,3) | C. | (6,3) | D. | (-6,-3) |

 如图,直角坐标平面内有两点A($\sqrt{3}$,1),B(1,$1\sqrt{3}$),将△AOB绕点O逆时针方向旋转150°得到△A′OB′,则线段AB的中点M所经过的路线长为$\frac{5\sqrt{6}+5\sqrt{2}}{12}$π.
如图,直角坐标平面内有两点A($\sqrt{3}$,1),B(1,$1\sqrt{3}$),将△AOB绕点O逆时针方向旋转150°得到△A′OB′,则线段AB的中点M所经过的路线长为$\frac{5\sqrt{6}+5\sqrt{2}}{12}$π. 对于正实数a,b;($\frac{a+b}{2}$)2-ab=$\frac{{a}^{2}+2ab+{b}^{2}}{4}$-$\frac{4ab}{4}$=$\frac{{a}^{2}-2ab+{b}^{2}}{4}$=($\frac{a-b}{2}$)2
对于正实数a,b;($\frac{a+b}{2}$)2-ab=$\frac{{a}^{2}+2ab+{b}^{2}}{4}$-$\frac{4ab}{4}$=$\frac{{a}^{2}-2ab+{b}^{2}}{4}$=($\frac{a-b}{2}$)2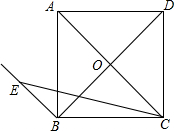 如图,四边形ABCD为正方形,EB∥AC,EC=AC,E在FB上,求∠ECB的度数.
如图,四边形ABCD为正方形,EB∥AC,EC=AC,E在FB上,求∠ECB的度数.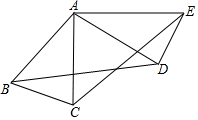 如图,△ABC中,AB=AC,∠ABC=70°.△ABC绕点A按逆时针方向旋转一定角度后,得到△ADE.问:
如图,△ABC中,AB=AC,∠ABC=70°.△ABC绕点A按逆时针方向旋转一定角度后,得到△ADE.问: