题目内容
8. 如图,直角坐标平面内有两点A($\sqrt{3}$,1),B(1,$1\sqrt{3}$),将△AOB绕点O逆时针方向旋转150°得到△A′OB′,则线段AB的中点M所经过的路线长为$\frac{5\sqrt{6}+5\sqrt{2}}{12}$π.
如图,直角坐标平面内有两点A($\sqrt{3}$,1),B(1,$1\sqrt{3}$),将△AOB绕点O逆时针方向旋转150°得到△A′OB′,则线段AB的中点M所经过的路线长为$\frac{5\sqrt{6}+5\sqrt{2}}{12}$π.
分析 首先根据中点坐标公式求出线段AB的中点M的坐标,再根据旋转的性质可知M所经过的路线是以O为圆心,圆心角为150°的一段圆弧,利用弧长公式即可求解.
解答 解:∵A($\sqrt{3}$,1),B(1,$1\sqrt{3}$),
∴线段AB的中点M的坐标是($\frac{\sqrt{3}+1}{2}$,$\frac{1+\sqrt{3}}{2}$),
∴OM=$\sqrt{(\frac{\sqrt{3}+1}{2})^{2}+(\frac{1+\sqrt{3}}{2})^{2}}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$,
∵将△AOB绕点O逆时针方向旋转150°得到△A′OB′,
∴线段AB的中点M所经过的路线长为$\frac{150π×\frac{\sqrt{6}+\sqrt{2}}{2}}{180}$=$\frac{5\sqrt{6}+5\sqrt{2}}{12}$π.
故答案为$\frac{5\sqrt{6}+5\sqrt{2}}{12}$π.
点评 本题考查了坐标与图形变化-旋转,中点坐标公式,弧长的计算公式,根据旋转的性质得出线段AB的中点M的运动轨迹是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
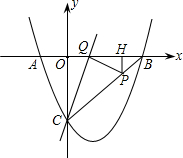 如图,已知抛物线y=$\frac{3}{4}{x}^{2}$+bx+c与轴交于A、B两点,与y轴交于C点,A的坐标为(-1,0),过点C的直线y=$\frac{3}{4t}$x-3与x轴交于点Q,点P是线段BC上的动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
如图,已知抛物线y=$\frac{3}{4}{x}^{2}$+bx+c与轴交于A、B两点,与y轴交于C点,A的坐标为(-1,0),过点C的直线y=$\frac{3}{4t}$x-3与x轴交于点Q,点P是线段BC上的动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
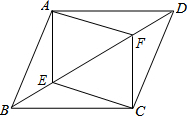 如图,在四边形ABCD中,点E,F是对角线BD上的两点,且BE=DF.
如图,在四边形ABCD中,点E,F是对角线BD上的两点,且BE=DF.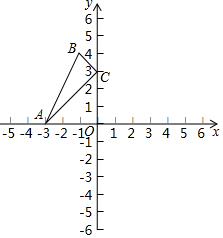 已知点A(-3,0),点C(0,3)且点B的坐标为(-1,4),计算△ABC的面积.
已知点A(-3,0),点C(0,3)且点B的坐标为(-1,4),计算△ABC的面积.