题目内容
9.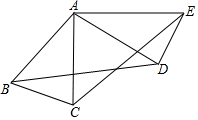 如图,△ABC中,AB=AC,∠ABC=70°.△ABC绕点A按逆时针方向旋转一定角度后,得到△ADE.问:
如图,△ABC中,AB=AC,∠ABC=70°.△ABC绕点A按逆时针方向旋转一定角度后,得到△ADE.问:(1)线段BD和CE相等吗?为什么?
(2)如果旋转角为80°,△CBD与△DCE是等腰三角形吗?为什么?
分析 (1)先根据图形旋转的性质得出∠BAD=∠CAE,再由SAS定理得出△ABD≌△ACE,由全等三角形的性质即可得出结论;
(2)根据等腰三角形的性质得到∠ABC=∠ACB=70°,由三角形的内角和得到∠BAC=40°,求得∠BAC=∠CAD,根据等腰三角形的性质得到AC垂直平分BD,根据线段垂直平分线的性质得到BC=CD,于是得到结论.
解答 解:(1)线段BD和CE相等,
理由:∵△ABC绕点A按逆时针方向旋转得△ADE,
∴∠BAD=∠CAE,
又∵AB=AC,
∴AB=AC=AD=AE.
在△ABD与△ACE中,
∵$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE(SAS).
∴BD=CE;
(2)△CBD与△DCE是等腰三角形,
理由:∵AB=AC,
∴∠ABC=∠ACB=70°,
∴∠BAC=40°,
∵∠BAD=80°,
∴∠CAD=40°,
∴∠BAC=∠CAD,
∵AB=AD,
∴AC垂直平分BD,
∴BC=CD,
同理CD=DE,
∴△CBD与△DCE是等腰三角形.
点评 本题考查的是旋转的性质,全等三角形的判定与性质,等腰三角形的性质,熟知图形旋转不变性的性质是解答此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
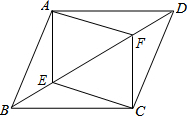 如图,在四边形ABCD中,点E,F是对角线BD上的两点,且BE=DF.
如图,在四边形ABCD中,点E,F是对角线BD上的两点,且BE=DF.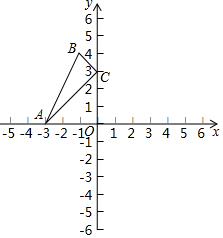 已知点A(-3,0),点C(0,3)且点B的坐标为(-1,4),计算△ABC的面积.
已知点A(-3,0),点C(0,3)且点B的坐标为(-1,4),计算△ABC的面积.