题目内容
19.a为何值时,方程|x-2|+2|x|+|x-1|=a有解?分析 把x分成x≤0,0<x<1和x≥2三种情况对方程进行讨论,进而确定a的范围.
解答 解:当x≤0时,原式即2-x-2x+1-x=a,
则-4x=a-3,
解得x=$\frac{3-a}{4}$,根据题意得$\frac{3-a}{4}$≤0,
解得a≥3;
当0<x<1时,原式即2-x+2x+1-x=a,此时a=3;
当x≥2时,原式即x-2+2x+x-1=a,
解得x=$\frac{a+3}{4}$,
则$\frac{a+3}{4}$≥2,
解得a≥5.
总之,当a≥3时,方程有解.
点评 本题考查了含有绝对值的方程的解的情况,正确进行讨论是关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
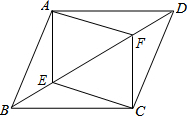 如图,在四边形ABCD中,点E,F是对角线BD上的两点,且BE=DF.
如图,在四边形ABCD中,点E,F是对角线BD上的两点,且BE=DF.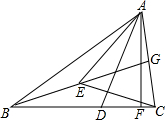 如图,在△ABC中,∠BAC=60°,∠ACB=80°,AD为∠BAC的角平分线,G、E分别是AC、BG的中点,AF⊥BC于F.求:
如图,在△ABC中,∠BAC=60°,∠ACB=80°,AD为∠BAC的角平分线,G、E分别是AC、BG的中点,AF⊥BC于F.求: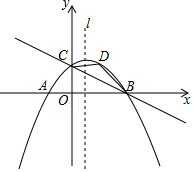 如图,已知抛物线y=-$\frac{1}{4}$x2+bx+c与y轴交于点C(0,2),与x轴交于A,B两点,点A的坐标为(-2,0).
如图,已知抛物线y=-$\frac{1}{4}$x2+bx+c与y轴交于点C(0,2),与x轴交于A,B两点,点A的坐标为(-2,0).