题目内容
15．
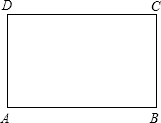如图长方形的周长为20，求长方形（1）面积的最大值．
（2）对角线的最小值．
分析 （1）先根据题意列出函数关系式，再求其最值即可；
（2）根据勾股定理列出函数关系式，再求其最值即可．
解答 解：（1）∵设矩形的一边长为x，则另一边长为10-x，
∴其面积为s=x（10-x）=-x2+10x=-（x-5）2+25，
∴当x=5时，s最大=25．
（2）设矩形的一边长为x，则另一边长为10-x，
∴对角线y2=x2+（10-x）2=2x2-20x+100=2（x-5）2+50，
∴当x=5时，y2最小=50，
∴对角线y的最小值为5$\sqrt{2}$．
点评 此题考查的是二次函数的最值问题，根据题意列出二次函数的解析式是解答此题的关键．
练习册系列答案
口算题天天练系列答案
相关题目
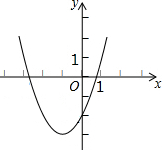抛物线y=ax2+bx+c的顶点为D（-1，-3），与x轴的一个交点A在点（-3，0）和（-2，0）之间，其部分图象如图所示，则以下结论：①abc＞0；②a+b+c＜0；③a-c=3；④方程以ax2+bx+c+3=0有两个的实根，其中正确的个数为（ ）
直线m的图象如图所示．试求y与x的函数关系式．小华的解法为：设y=kx．由图象可得2=3k．故k=$\frac{2}{3}$．所以y与x的函数关系式为y=$\frac{2}{3}$x，请你评判小华的做法，如果不正确．请给出正确的作法．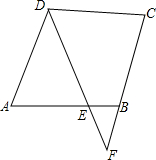
如图，在?ABCD中，AD=4，AE：CD=2：3，DE与CB的延长线交于点F，求CF的长．
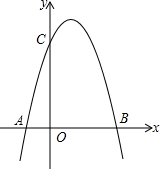如图，二次函数的图象经过A、B、C三点，点A的坐标为（-1，0），点B的坐标为（4，0），点C在y轴正半轴上，且OB=OC．
今有邑方不知大小，各开中门，出北门三十步有木，出西门七百五十步见木，问：邑方几何？
7．在平面直角坐标系中，设点A（-8，3）、B（-4，5）及动点C（0，n），D （m，0），当四边形ABCD的周长最小时，C、D的位置的确定方法正确的是（ ）
| A． | 作点A关于x轴的对称点A′，点B关于y轴的对称点B′，连接A′B′交x轴于点D，交y轴于C | |
| B． | 作点A关于x轴的对称点A′，点B关于y轴的对称点B′，连接A′B′交x轴于点C，交y轴于D | |
| C． | 过A作AD⊥x轴于D点，过B作BC⊥y轴于C点 | |
| D． | 过A作AC⊥x轴于C点，过B作BD⊥y轴于D点 |
5．在下列表述中，不能表示式子5a的是（ ）
| A． | 5的a倍 | B． | a的5倍 | C． | 5个a相加 | D． | 5个a相乘 |