题目内容
3.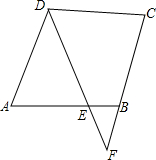 如图,在?ABCD中,AD=4,AE:CD=2:3,DE与CB的延长线交于点F,求CF的长.
如图,在?ABCD中,AD=4,AE:CD=2:3,DE与CB的延长线交于点F,求CF的长.
分析 根据平行四边形性质得出AD=BC=4,AB=DC,AB∥CD,推出△FEB∽△FDC,根据相似三角形的性质得到$\frac{BE}{CD}=\frac{BF}{CF}$,代入求出即可.
解答 解:∵四边形ABCD是平行四边形,
∴AD=BC=4,AB=DC,AB∥CD,
∵AE:CD=2:3,
∴$\frac{BE}{CD}$=$\frac{1}{3}$,
∴△FEB∽△FDC,
∴$\frac{BE}{CD}=\frac{BF}{CF}$,
即:$\frac{CF-4}{CF}$=$\frac{1}{3}$,
∴CF=6.
点评 本题考查了平行四边形性质,相似三角形的性质和判定的应用,关键是证出△FEB∽△FDC.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11. 如图,在⊙O中,AB=CD,则下列结论错误的是( )
如图,在⊙O中,AB=CD,则下列结论错误的是( )
 如图,在⊙O中,AB=CD,则下列结论错误的是( )
如图,在⊙O中,AB=CD,则下列结论错误的是( )| A. | $\widehat{AB}=\widehat{CD}$ | B. | $\widehat{AC}$=$\widehat{BD}$ | C. | AC=BD | D. | AD=BD |
 如图,点P为⊙0外一点,PC与⊙0相切于点C,PO的延长线交⊙0于E,⊙0的半径为3,PC=4,求CE的长.
如图,点P为⊙0外一点,PC与⊙0相切于点C,PO的延长线交⊙0于E,⊙0的半径为3,PC=4,求CE的长.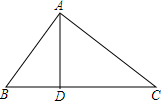 已知:如图,在△ABC中,AD⊥BC,垂足为D,且BC=16,AB=DC,cos∠ABC=$\frac{3}{5}$.(1)求:BD的长;(2)求:tanC的值.
已知:如图,在△ABC中,AD⊥BC,垂足为D,且BC=16,AB=DC,cos∠ABC=$\frac{3}{5}$.(1)求:BD的长;(2)求:tanC的值.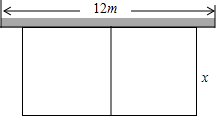 有长24m的篱笆,一面利用长为12m的围墙围成如图所示中间隔有一道篱笆的矩形花圃.设花圃垂直于墙的一边长为xm,面积为Sm2.则S与x的函数关系式是S=(24-3x)x,x的取值范围为4≤x<8.
有长24m的篱笆,一面利用长为12m的围墙围成如图所示中间隔有一道篱笆的矩形花圃.设花圃垂直于墙的一边长为xm,面积为Sm2.则S与x的函数关系式是S=(24-3x)x,x的取值范围为4≤x<8.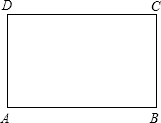 如图长方形的周长为20,求长方形
如图长方形的周长为20,求长方形