题目内容
20. 今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?
今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?
分析 根据题意得出:△DEC∽△DBF,结合相似三角形的性质,进而求出答案.
解答  解:延长BA,DC,相交于点F,
解:延长BA,DC,相交于点F,
由题意可得:四边形ECFA是正方形,
设EC=AF=FC=x,
可得:△DEC∽△DBF,
故$\frac{DC}{DF}$=$\frac{EC}{BF}$,
则$\frac{750}{750+x}$=$\frac{x}{30+x}$,
解得:x=150,
故正方形的边长为:300步.
点评 此题主要考查了相似三角形的应用,正确利用相似三角形的判定与性质是解题关键.

练习册系列答案
相关题目
10.某电脑公司准备每周(按120个工时计算)组装三种型号的电脑360台,组装这些电脑每台所需工时和每台产值如下表.
(1)如果每周准备组装100台型号③电脑,那么每周应组装型号①、②电脑各几台?
(2)如果一周产值定为10万元,那么这周应组装型号①、②、③电脑各几台?
(3)若一周型号③电脑至少组装20台,一周产值记为w,试直接写出w的范围.
| 电脑型号 | ① | ② | ③ |
| 工时(个) | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{4}$ |
| 产值(万元) | 0.4 | 0.3 | 0.2 |
(2)如果一周产值定为10万元,那么这周应组装型号①、②、③电脑各几台?
(3)若一周型号③电脑至少组装20台,一周产值记为w,试直接写出w的范围.
11. 如图,在⊙O中,AB=CD,则下列结论错误的是( )
如图,在⊙O中,AB=CD,则下列结论错误的是( )
 如图,在⊙O中,AB=CD,则下列结论错误的是( )
如图,在⊙O中,AB=CD,则下列结论错误的是( )| A. | $\widehat{AB}=\widehat{CD}$ | B. | $\widehat{AC}$=$\widehat{BD}$ | C. | AC=BD | D. | AD=BD |
8.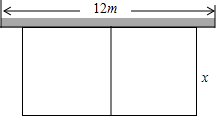 有长24m的篱笆,一面利用长为12m的围墙围成如图所示中间隔有一道篱笆的矩形花圃.设花圃垂直于墙的一边长为xm,面积为Sm2.则S与x的函数关系式是S=(24-3x)x,x的取值范围为4≤x<8.
有长24m的篱笆,一面利用长为12m的围墙围成如图所示中间隔有一道篱笆的矩形花圃.设花圃垂直于墙的一边长为xm,面积为Sm2.则S与x的函数关系式是S=(24-3x)x,x的取值范围为4≤x<8.
 有长24m的篱笆,一面利用长为12m的围墙围成如图所示中间隔有一道篱笆的矩形花圃.设花圃垂直于墙的一边长为xm,面积为Sm2.则S与x的函数关系式是S=(24-3x)x,x的取值范围为4≤x<8.
有长24m的篱笆,一面利用长为12m的围墙围成如图所示中间隔有一道篱笆的矩形花圃.设花圃垂直于墙的一边长为xm,面积为Sm2.则S与x的函数关系式是S=(24-3x)x,x的取值范围为4≤x<8.
9.在Rt△ABC中,∠C=90°,点D是斜边AB的中点,若BC=6,CD=5,则cosB的值为( )
| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
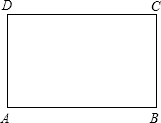 如图长方形的周长为20,求长方形
如图长方形的周长为20,求长方形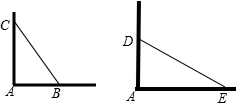 一架梯子长15m,如图甲所示斜靠在墙上,梯子底端离墙7m.
一架梯子长15m,如图甲所示斜靠在墙上,梯子底端离墙7m. 如图,在△ABC中,BC=5cm,边长为2cm的正方形DEFG的一边EF在BC上,点D在AB上,点G在AC上,求△ABC的面积.
如图,在△ABC中,BC=5cm,边长为2cm的正方形DEFG的一边EF在BC上,点D在AB上,点G在AC上,求△ABC的面积.