题目内容
5.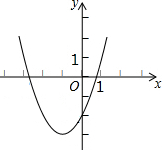 抛物线y=ax2+bx+c的顶点为D(-1,-3),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图所示,则以下结论:①abc>0;②a+b+c<0;③a-c=3;④方程以ax2+bx+c+3=0有两个的实根,其中正确的个数为( )
抛物线y=ax2+bx+c的顶点为D(-1,-3),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图所示,则以下结论:①abc>0;②a+b+c<0;③a-c=3;④方程以ax2+bx+c+3=0有两个的实根,其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 抛物线开口向上a>0,对称轴在y轴左侧,b>0,抛物线和y轴负半轴相交,c<0,则abc<0,由抛物线与x轴有两个交点得到b2-4ac>0;有抛物线顶点坐标得到抛物线的对称轴为直线x=-1,则根据抛物线的对称性得抛物线与x轴的另一个交点在点(-3,0)和(-2,0)之间,所以当x=1时,y>0,则a+b+c>0;由抛物线的顶点为D(-1,-3)得a-b+c=-3,由抛物线的对称轴为直线x=-$\frac{b}{2a}$=-1得b=2a,所以a-c=3;根据二次函数的最大值问题,当x=-1时,二次函数有最大值为-3,即b2-4ac=-12a,b2-4a(c+3)=b2-4ac-12a=-24a,所以说方程ax2+bx+c+3=0无实数根.
解答 解:∵抛物线开口向上,
∴a>0,
∵对称轴在y轴左侧,
∴b>0,
∵抛物线和y轴负半轴相交,
∴c<0,
∴abc<0,故①错误;
∵当x=1时,y>0,
∴y=a+b+c>0,故②错误;
∵抛物线的顶点为D(-1,-3)
∴a-b+c=-3,
∵抛物线的对称轴为直线x=-$\frac{b}{2a}$=-1得b=2a,
把b=2a代入a-b+c=-3,得a-2a+c=-3,
∴c-a=-3,
∴a-c=3,故③正确;
∵二次函数y=ax2+bx+c有最大值为-3,
∴b2-4ac=-12a,
∴方程ax2+bx+c+3=0的判别式△=b2-4a(c+3)=b2-4ac-12a=-24a<0,
∴方程ax2+bx+c+3=0无实数根,故④错误;
故选A.
点评 本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-$\frac{b}{2a}$;抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点.

 作业辅导系列答案
作业辅导系列答案| 电脑型号 | ① | ② | ③ |
| 工时(个) | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{4}$ |
| 产值(万元) | 0.4 | 0.3 | 0.2 |
(2)如果一周产值定为10万元,那么这周应组装型号①、②、③电脑各几台?
(3)若一周型号③电脑至少组装20台,一周产值记为w,试直接写出w的范围.
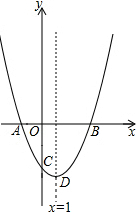 已知二次函数图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点是点D,其中A(-1,0),C(0,-3),对称轴是直线x=1.
已知二次函数图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点是点D,其中A(-1,0),C(0,-3),对称轴是直线x=1. 如图,点P为⊙0外一点,PC与⊙0相切于点C,PO的延长线交⊙0于E,⊙0的半径为3,PC=4,求CE的长.
如图,点P为⊙0外一点,PC与⊙0相切于点C,PO的延长线交⊙0于E,⊙0的半径为3,PC=4,求CE的长.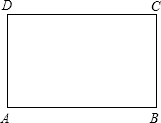 如图长方形的周长为20,求长方形
如图长方形的周长为20,求长方形