题目内容
(1)计算:
-(
)-1-2tan60°+3÷
×2.
(2)解方程:
-
-1=0.
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)解方程:
| x+1 |
| 2x-1 |
| 4x-2 |
| x+1 |
考点:实数的运算,负整数指数幂,换元法解分式方程,特殊角的三角函数值
专题:
分析:(1)原式第一项化为最简二次根式,第二项利用负指数幂法则计算,第三项利用特殊角的三角函数值计算,最后一项利用乘除法则计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答:解:(1)原式=2
-2-2
+12=10;
(2)去分母得:x2+2x+1-2(4x2-4x+1)-2x2-2x+x+1=0,
整理得:-9x2-9x=0,即-9x(x+1)=0,
解得:x1=0,x2=1,
经检验x=0或x=1都为分式方程的解.
| 3 |
| 3 |
(2)去分母得:x2+2x+1-2(4x2-4x+1)-2x2-2x+x+1=0,
整理得:-9x2-9x=0,即-9x(x+1)=0,
解得:x1=0,x2=1,
经检验x=0或x=1都为分式方程的解.
点评:此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
下列每组数分别是三条线段的长度(单位:cm),它们首尾相连能围成三角形的是( )
| A、3,3,5 |
| B、1,10,12 |
| C、8,11,20 |
| D、7,8,15 |
已知关于x的一元二次方程x2+6x+5=0有两个根为x1和x2,则x1x2+x1+x2的值是( )
| A、5 | B、-5 | C、1 | D、-1 |
若不等式x<3的解都能使关于x的一次不等式(a-1)x<a+3成立,则a的取值范围是( )
| A、1<a<3 |
| B、a<1或a>3 |
| C、1≤a<3 |
| D、1<a≤3 |
 如图,某大楼顶部有一旗杆AB,甲乙两人分别在相距6米的C、D两处测得B点和A点的仰角分别是42°和65°,且C、D、E在一条直线上.如果DE=15米,求旗杆AB的长大约是多少米?(结果保留整数)
如图,某大楼顶部有一旗杆AB,甲乙两人分别在相距6米的C、D两处测得B点和A点的仰角分别是42°和65°,且C、D、E在一条直线上.如果DE=15米,求旗杆AB的长大约是多少米?(结果保留整数) 如图,已知函数y=2x+b与函数y=kx-3的图象交于点P,则不等式kx-3<2x+b的解集是
如图,已知函数y=2x+b与函数y=kx-3的图象交于点P,则不等式kx-3<2x+b的解集是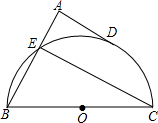 如图,BC是半圆的直径,点D是半圆上的一点,过D作圆O的切线AD,BA垂直DA于点A,BA交半圆于点E,已知BC=10,AD=4,那么直线CE与以点O为圆心、
如图,BC是半圆的直径,点D是半圆上的一点,过D作圆O的切线AD,BA垂直DA于点A,BA交半圆于点E,已知BC=10,AD=4,那么直线CE与以点O为圆心、