题目内容
16. 如图,正方形AOBC在第一象限内,点C(2,2),E是边OB上的动点(不包括端点),作∠AEF=90°,且使AE=EF,请你画出点F的纵坐标随着横坐标变化的函数图象.
如图,正方形AOBC在第一象限内,点C(2,2),E是边OB上的动点(不包括端点),作∠AEF=90°,且使AE=EF,请你画出点F的纵坐标随着横坐标变化的函数图象.
分析 作FG⊥x轴于G,先证明△AOE≌△EGF,再证明BF平分∠CBG即可,求出直线BF的解析式即可,注意自变量的取值范围.
解答 解:作FG⊥x轴于G.
∵∠AEF═∠EGF=90°,
∴∠AEO+∠FEG=90°,∠FEG+∠FGE=90°,
∴∠AEO=∠FGE,
在△AEO和△EFG中,
$\left\{\begin{array}{l}{∠AEO=∠EFG}\\{∠AOE=∠EGF=90°}\\{AE=EF}\end{array}\right.$,
∴△AOE≌△EGF,
∴OE=FG,AO=EG=OB,
∴OE=BG=FG,
∴∠GBF=45°,
∴BF平分∠CBG,
∴点F在∠CBG的平分线上,设直线BF解析式为y=kx+b,
设E(a,0)(0<a<2)
∴EO=FG=a; AO=EG=2
∴OG=a+2
∴F(a+2,a)
则$\left\{\begin{array}{l}{(a+2)k+b=a}\\{2k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$
∴直线BF的解析式为y=x-2,(2<x<4),
点F的纵坐标随着横坐标变化的函数图象如图所示.
点评 本题考查正方形的性质、全等三角形的判定和性质、一次函数的性质等知识,解题的关键是正确寻找全等三角形,易错点是自变量的范围的确定,属于中考常考题型.

练习册系列答案
相关题目
4. 如图,已知长方体ABCD-EFGH,那么下列直线中与直线BC异面的是( )
如图,已知长方体ABCD-EFGH,那么下列直线中与直线BC异面的是( )
 如图,已知长方体ABCD-EFGH,那么下列直线中与直线BC异面的是( )
如图,已知长方体ABCD-EFGH,那么下列直线中与直线BC异面的是( )| A. | EF | B. | AD | C. | CG | D. | EH |
 如图,在Rt△ABC中,AC=2,斜边AB=$\sqrt{13}$,延长AB到点D,使BD=AB,连接CD,则tan∠BCD=$\frac{1}{3}$.
如图,在Rt△ABC中,AC=2,斜边AB=$\sqrt{13}$,延长AB到点D,使BD=AB,连接CD,则tan∠BCD=$\frac{1}{3}$.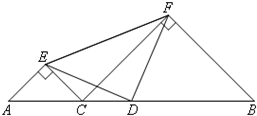 已知:如图,D为线段AB的中点,在AB上任取一点C(不与点A,B,D重合),分别以AC,BC为斜边在AB同侧作等腰Rt△ACE与等腰Rt△BCF,∠AEC=∠CFB=90°,连接DE,DF,EF.
已知:如图,D为线段AB的中点,在AB上任取一点C(不与点A,B,D重合),分别以AC,BC为斜边在AB同侧作等腰Rt△ACE与等腰Rt△BCF,∠AEC=∠CFB=90°,连接DE,DF,EF. 如图,一块大的三角板ABC,D是AB上一点,现要求过点D割出一块小的三角板ADE,使∠ADE=∠ABC,
如图,一块大的三角板ABC,D是AB上一点,现要求过点D割出一块小的三角板ADE,使∠ADE=∠ABC, 如图,两张48×40的长方形纸片有一个顶点重合,重叠放置的尺寸如图所标示,则图中阴影部分的面积=984.
如图,两张48×40的长方形纸片有一个顶点重合,重叠放置的尺寸如图所标示,则图中阴影部分的面积=984.
 如图,直线AB∥CD,AG⊥EF,垂足为G,则图中与∠GAH互余的角是∠FHB,∠AEH,∠EGC,∠DGH.
如图,直线AB∥CD,AG⊥EF,垂足为G,则图中与∠GAH互余的角是∠FHB,∠AEH,∠EGC,∠DGH.