题目内容
9.如果把一个奇数位的自然数各数为上的数字从最高位到个位依次排列,与从个位到最高位依次排列出的一串数字完全相同,相邻两个数位上的数字之差的绝对值相等(不等于0),且该数正中间的数字与其余数字均不同,我们把这样的自然数称为“阶梯数”,例如自然数12321,从最高位到个位依次排出的一串数字是:1,2,3,2,1,从个位到最高位依次排出的一串数字仍是:1,2,3,2,1,且|1-2|=|2-3|=|3-2|=|2-1|=1,因此12321是一个“阶梯数”,又如262,85258,…,都是“阶梯数”,若一个“阶梯数”t从左数到右,奇数位上的数字之和为M,偶数位上的数字之和为N,记P(t)=2N-M,Q(t)=M+N.(1)已知一个三位“阶梯数”t,其中P(t)=12,且Q(t)为一个完全平方数,求这个三位数;
(2)已知一个五位“阶梯数”t能被4整除,且Q(t)除以4余2,求该五位“阶梯数”t的最大值与最小值.
分析 (1)设“阶梯数”t的百位为x,相邻两数的差为k,则t=$\overline{a(a+k)a}$,可得M=a+a=2a,N=a+k,根据P(t)=12,得到关于k的方程,可求k=6,再根据Q(t)=3a+6为一个完全平方数,其中1≤a≤9,可求3a+6=9,16,25,可求a=1,从而得到这个三位数;
(2)设某五位阶梯数为$\overline{a(a+k)(a+2k)(a+k)a}$,根据$\frac{t}{4}$=$\frac{11111a+1210k}{4}$=2778a+302k+$\frac{2k-a}{4}$,
可得2k-a是4的倍数,根据M=3a+2k,N=2A+2K,可得Q(t)=M+N=5a+4k,则$\frac{5a+4k-2}{4}$=k+a+$\frac{a-2}{4}$,可得a-2是4的倍数,根据完全平方数的定义得到a=2,6,再分两种情况求得t的值,进一步得到该五位“阶梯数”t的最大值和最小值.
解答 解:(1)设“阶梯数”t的百位为x,相邻两数的差为k,则t=$\overline{a(a+k)a}$,
∴M=a+a=2a,N=a+k,
∴P(t)=2N-M=2(a+k)-2a=2k=12,
∴k=6,
∵Q(t)=M+N=2a+a+k=3a+6为一个完全平方数,其中1≤a≤9,
∴9≤3a+6≤33,
∴3a+6=9,16,25,
∴a=1,
∴t=171;
(2)设某五位阶梯数为$\overline{a(a+k)(a+2k)(a+k)a}$,
∵$\frac{t}{4}$=$\frac{11111a+1210k}{4}$=2778a+302k+$\frac{2k-a}{4}$,
∴2k-a是4的倍数,
∵M=3a+2k,N=2A+2K,
∴Q(t)=M+N=5a+4k,
∴$\frac{5a+4k-2}{4}$=k+a+$\frac{a-2}{4}$,
∴a-2是4的倍数,
∵1≤a≤9,
∴-1≤a-2≤7,
∴a-2=0,4,
∴a=2,6
当a=2时,$\frac{2k-2}{4}$为整数且0≤2+2k≤9,
∴-1≤k≤$\frac{7}{2}$,
∴k=±1,3,
所以t=21012,23432,25852;
当a=6时,$\frac{2k-6}{4}$为整数且0≤6+2k≤9,
∴-3≤k≤$\frac{3}{2}$,
∴k=±1,-3,
所以t=63036,65456,67876.
所以该五位“阶梯数”t的最大值是67876,最小值是21012.
点评 考查了完全平方数,解题的关键是弄清楚“阶梯数”的定义,从而写出符合题意的数.

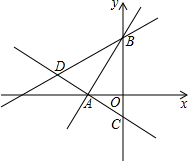 如图,在平面直角坐标系中,已知点A(-$\sqrt{3}$,0),B(0,3),C(0,-1)三点.
如图,在平面直角坐标系中,已知点A(-$\sqrt{3}$,0),B(0,3),C(0,-1)三点.


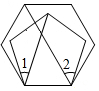 正五边形和正六边形按如图所示的位置进行摆放,则∠2-∠1的度数为34°.
正五边形和正六边形按如图所示的位置进行摆放,则∠2-∠1的度数为34°.