题目内容
11.计算题(1)$\frac{2\sqrt{12}+\sqrt{3}}{\sqrt{3}}$+(1-$\sqrt{3}$)0
(2)已知:x=$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$,y=$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$,求$\frac{{x}^{3}-x{y}^{2}}{{x}^{4}y+2{x}^{3}{y}^{2}+{x}^{2}{y}^{3}}$的值.
分析 (1)首先分母有理化,计算0次幂,然后进行加减即可;
(2)首先对x和y进行分母有理化,然后把所求的分式约分,然后代入x和y的数值计算即可.
解答 解:(1)原式=$\frac{12+3}{3}$+1=5+1=6;
(2)x=($\sqrt{3}$+$\sqrt{2}$)2=5+2$\sqrt{6}$,y=($\sqrt{3}$-$\sqrt{2}$)2=5-2$\sqrt{6}$,
则原式=$\frac{x(x+y)(x-y)}{{x}^{2}y(x+y)^{2}}$=$\frac{x-y}{xy(x+y)}$,
则当x=5+2$\sqrt{6}$,y=5-2$\sqrt{6}$时,原式=$\frac{(5+2\sqrt{6})-(5-2\sqrt{6})}{(5+2\sqrt{6})(5-2\sqrt{6})(5+2\sqrt{6}+5-2\sqrt{6})}$=$\frac{4\sqrt{6}}{10}$=$\frac{2\sqrt{6}}{5}$.
点评 本题考查了二次根式的化简求值以及分式的化简求值,正确对分式进行化简、对分子和分母分解因式是关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
19.下列图形中,轴对称图形的个数为( )

| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
16.-2015的倒数是( )
| A. | 2015 | B. | -$\frac{1}{2015}$ | C. | $\frac{1}{2015}$ | D. | -2015 |
3.下列运算正确的是( )
| A. | a-1÷a3=a2 | B. | ($\frac{1}{3}$)0=0 | C. | 3-2=$\frac{1}{9}$ | D. | (a2)3=a5 |
20.下列长度的三条线段能构成三角形的是( )
| A. | 3,4,8 | B. | 3,4,7 | C. | 5,6,10 | D. | 5,6,11 |
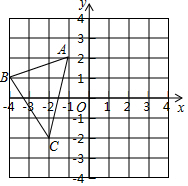 如图,已知△ABC的三个顶点的坐标为A(-1,2),B(-4,1),C(-2,-2).
如图,已知△ABC的三个顶点的坐标为A(-1,2),B(-4,1),C(-2,-2).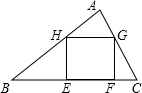 如图,在Rt△ABC中,∠A=90°,正方形EFGH的四个顶点在三角形的边上,已知BE=6,FC=2,则正方形EFGH的边长等于2$\sqrt{3}$.
如图,在Rt△ABC中,∠A=90°,正方形EFGH的四个顶点在三角形的边上,已知BE=6,FC=2,则正方形EFGH的边长等于2$\sqrt{3}$.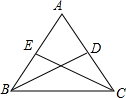 如图,在△ABC中,AB=AC,BD和CE是△ABC的两条角平分线.(请填空)
如图,在△ABC中,AB=AC,BD和CE是△ABC的两条角平分线.(请填空)