题目内容
17.已知a,b,c是三角形的三边,且(b-1)2+|a2-9|=0,则第三边c的范围是2<c<4.分析 先根据(b-1)2+|a2-9|=0,求得b=1,a=3,再根据三角形的三边关系,求得第三边c的范围.
解答 解:∵(b-1)2+|a2-9|=0,
∴b-1=0,a2-9=0,
∴b=1,a=3,(a=-3舍去)
∵a,b,c是三角形的三边,
∴3-1<c<3+1,
∴2<c<4,
故答案为:2<c<4.
点评 本题主要考查了三角形的三边关系以及非负数的性质,解决问题的关键是掌握:三角形两边之和大于第三边,三角形的两边差小于第三边.

练习册系列答案
相关题目
2.在△ABC中,∠C=90°,AB=6,BC=4,则tanB的值是( )
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{5}}{2}$ |
6. 如图,在△ABC中,D、E分别是AC、AB上的点,在△ADE≌△BDE≌△BDC,则∠A的度数是( )
如图,在△ABC中,D、E分别是AC、AB上的点,在△ADE≌△BDE≌△BDC,则∠A的度数是( )
 如图,在△ABC中,D、E分别是AC、AB上的点,在△ADE≌△BDE≌△BDC,则∠A的度数是( )
如图,在△ABC中,D、E分别是AC、AB上的点,在△ADE≌△BDE≌△BDC,则∠A的度数是( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
 如图,△ABC在直角坐标系中,现另有一点D满足A,B,D为顶点的三角形与△ABC全等,则满足条件的D点的个数为3.
如图,△ABC在直角坐标系中,现另有一点D满足A,B,D为顶点的三角形与△ABC全等,则满足条件的D点的个数为3.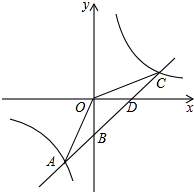 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.