题目内容
2.在△ABC中,∠C=90°,AB=6,BC=4,则tanB的值是( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{5}}{2}$ |
分析 首先利用勾股定理求得AC的长,然后利用正切函数的定义求解.
解答  解:AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$,
解:AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$,
则tanB=$\frac{AC}{BC}$=$\frac{2\sqrt{5}}{4}$=$\frac{\sqrt{5}}{2}$.
故选D.
点评 本题考查了三角函数的定义以及勾股定理,正确记忆正切函数的定义是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知等腰△ABC中,AB=AC,点D为BC边上一点,连接AD,若△ACD和△ABD都是等腰三角形,则∠ACB的度数为( )
| A. | 36° | B. | 45° | C. | 36°或45° | D. | 36°或45°或72° |
12.在直角坐标系中,点A(-2,3)与点B关于原点成中心对称,则点B的坐标为( )
| A. | (2,3) | B. | (2,-3) | C. | (-2,-3) | D. | (-2,3) |
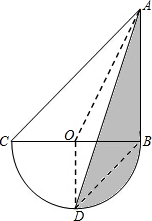 如图,三角形ABC是等腰直角三角形,D是圆周的中点,BC是半圆的直径,已知AB=BC=10厘米,那么阴影部分面积是多少?
如图,三角形ABC是等腰直角三角形,D是圆周的中点,BC是半圆的直径,已知AB=BC=10厘米,那么阴影部分面积是多少?