题目内容
5.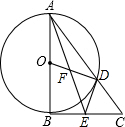 如图,在△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是BC的中点,连接AE、OD、DE、AE与OD相交于F.
如图,在△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是BC的中点,连接AE、OD、DE、AE与OD相交于F.(1)求证:DE是⊙O的切线;
(2)若AB=10,OF=2,求AD的长;
(3)四边形AOED是平行四边形时,求sin∠CAE的值.
分析 (1)连结OE,如图,先根据圆周角定理,由AB为直径得到∠ADB=90°,再根据直角三角形斜边上的中线性质得BE=DE=CE,然后证明△ABE≌△ODE得到∠OBE=∠ODE=90°,再利用切线的判定定理判断DE是⊙O的切线;
(2)先证明OE为△BAC的中位线,得到OE∥AC,OE=$\frac{1}{2}$AC,利用平行线分线段成比例定理得出$\frac{OE}{AD}=\frac{OF}{DF}$=$\frac{2}{3}$,设OE=2x,则AD=3x,AC=4x,CD=AC-AD=x,证明Rt△CBD∽Rt△CAB,得出对应边成比例求出BC=2x,由勾股定理求出AB=2$\sqrt{3}$x=10,得出x的值,即可得出结果;
(3)作EH⊥AC于H,由平行四边形的性质得出AB∥DE,得出DE⊥BC,证出△BDC为等腰直角三角形,CH=DH,得出△CEH和△ABC都是等腰直角三角形,设⊙O的半径为r,则AB=2r,AD=CD=$\sqrt{2}$r,CH=DH=$\frac{\sqrt{2}}{2}$r,得出EH=CH=$\frac{\sqrt{2}}{2}$r,由勾股定理求出AE,再由三角函数定义即可得出结果.
解答 (1)证明:连结OE,如图1,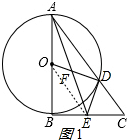
∵AB为直径,
∴∠ADB=90°,
∵E是Rt△BCD斜边BC的中点,
∴BE=DE=CE,
在△ABE和△ODE中,$\left\{\begin{array}{l}{OB=OD}&{\;}\\{BE=DE}&{\;}\\{OE=OE}&{\;}\end{array}\right.$,
∴△ABE≌△ODE(SSS),
∴∠OBE=∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:∵AB=10,OF=2,
∴DF=5-2=3,
∵OA=OB,BE=CE,
∴OE为△BAC的中位线,
∴OE∥AC,OE=$\frac{1}{2}$AC,
∵OE∥AD,
∴$\frac{OE}{AD}=\frac{OF}{DF}$=$\frac{2}{3}$,
设OE=2x,则AD=3x,AC=4x,
∴CD=AC-AD=x,
∵∠BCD=∠ACB,
∴Rt△CBD∽Rt△CAB,
∴$\frac{CD}{CB}=\frac{CB}{CA}$,即$\frac{x}{cb}=\frac{CB}{4x}$,
解得:BC=2x,
在Rt△ABC中,∵AC=4x,BC=2x,
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=2$\sqrt{3}$x,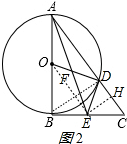
∴2$\sqrt{3}$x=10,
解得:x=$\frac{5\sqrt{3}}{3}$,
∴AC=4x=$\frac{20\sqrt{3}}{3}$;
(3)解:作EH⊥AC于H,如图2,
∵四边形AOED是平行四边形,
∴AB∥DE,
∴DE⊥BC,
而BE=CE,
∴△BDC为等腰直角三角形,CH=DH,
∴∠C=45°,
∴△CEH和△ABC都是等腰直角三角形,
设⊙O的半径为r,则AB=2r,AD=CD=$\sqrt{2}$r,CH=DH=$\frac{\sqrt{2}}{2}$r,
∴EH=CH=$\frac{\sqrt{2}}{2}$r,
∴AH=$\sqrt{2}$r+$\frac{\sqrt{2}}{2}$r=$\frac{3\sqrt{2}}{2}$r,
∴AE=$\sqrt{A{H}^{2}+E{H}^{2}}$=$\sqrt{5}$r,
在Rt△AEH中,sin∠HAE=$\frac{EH}{AE}$=$\frac{\frac{\sqrt{2}}{2}r}{\sqrt{5}r}$=$\frac{\sqrt{10}}{10}$,
即sin∠CAE的值为$\frac{\sqrt{10}}{10}$.
点评 本题考查了切线的判定、全等三角形的判定与性质、相似三角形的判定与性质、三角形中位线定理、平行四边形的性质、平行线分线段成比例定理、等腰直角三角形的判定与性质、勾股定理等知识;本题综合性强,难度较大,特别是(2)(3)中,需要证明三角形相似、等腰直角三角形和运用勾股定理才能得出结果.

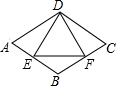 如图所示,菱形ABCD的周长为16cm,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为E,F,则△DEF的周长为6$\sqrt{3}$cm.
如图所示,菱形ABCD的周长为16cm,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为E,F,则△DEF的周长为6$\sqrt{3}$cm.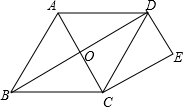 如图,O是菱形ABCD的对角线的交点,BC=2OC=2,DE=1,DE∥AC,
如图,O是菱形ABCD的对角线的交点,BC=2OC=2,DE=1,DE∥AC,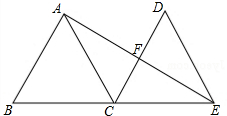 如图,等边△ABC的边长为6,现将△ABC沿直线向右平移,使点B与点C重合,得△DCE,连结AE交DC于点F.
如图,等边△ABC的边长为6,现将△ABC沿直线向右平移,使点B与点C重合,得△DCE,连结AE交DC于点F.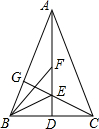 如图,△ABC中,AB=AC,AD⊥BC于点D,射线BE、BF将∠ABC三等分交AD于E、F两点,连接CE并延长交AB于点G,求证:$\frac{AF}{EF}$=$\frac{AG}{GB}$.
如图,△ABC中,AB=AC,AD⊥BC于点D,射线BE、BF将∠ABC三等分交AD于E、F两点,连接CE并延长交AB于点G,求证:$\frac{AF}{EF}$=$\frac{AG}{GB}$. 如图,已知∠BAC=∠ACD,则可判断图中AB∥CD.
如图,已知∠BAC=∠ACD,则可判断图中AB∥CD.