题目内容
8.若二元二次方程组$\left\{\begin{array}{l}{{x}^{2}{-y}^{2}=1}\\{y=k(x-2)+1}\end{array}\right.$有唯一解,求实数k的值.分析 先利用代入消元法得到(1-k2)x2+2k(2k-1)x-4k2+4k-2=0,再分类讨论:当1-k2=0时,即k=±1,关于x的方程变形为一元一次方程,方程有一个解,则方程组有唯一解;当1-k2≠0时,关于x的方程变形为一元二次方程,当△=0时,方程有两组相同的解,方程组有唯一解,所以[2k(2k-1)]2-4(1-k2)(-4k2+4k-2)=0,整理得3k2-4k+2=0,而此方程无实数根,然后综合两种情况得到k=±1.
解答 解:$\left\{\begin{array}{l}{{x}^{2}-{y}^{2}=1}&{①}\\{y=k(x-2)+1}&{②}\end{array}\right.$,
把②代入①得x2-[k(x-2)+1]2=1,
整理得(1-k2)x2+2k(2k-1)x-4k2+4k-2=0,
当1-k2=0时,即k=±1,关于x的方程变形为一元一次方程,方程有一个解;
当1-k2≠0时,即k≠±1,关于x的方程变形为一元二次方程,
当△=0时,方程有两组相同的解,即[2k(2k-1)]2-4(1-k2)(-4k2+4k-2)=0,
整理得3k2-4k+2=0,此方程无实数根,
所以当k=1或-1时,原方程组有唯一解.
点评 本题考查了高次方程:通过适当的方法,把高次方程化为次数较低的方程求解.所以解高次方程一般要降次,即把它转化成二次方程或一次方程.也有的通过因式分解来解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图,△ABC中,∠C=90°,AC=3cm,点P是边BC上的动点,则AP长不可能是( )
如图,△ABC中,∠C=90°,AC=3cm,点P是边BC上的动点,则AP长不可能是( )
 如图,△ABC中,∠C=90°,AC=3cm,点P是边BC上的动点,则AP长不可能是( )
如图,△ABC中,∠C=90°,AC=3cm,点P是边BC上的动点,则AP长不可能是( )| A. | 2.5cm | B. | 3cm | C. | 4cm | D. | 5cm |
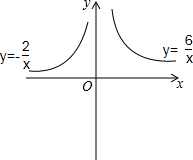 如图,在平面直角坐标系中,动点A从原点O出发沿y轴正半轴以每秒1单位长度运动,运动的时间为t秒,过点A作x轴的平行线,交函数y=-$\frac{2}{x}$(x<0)的图象于B,交函数y=$\frac{6}{x}$(x>0)的图象于C,作射线BO,点D是射线BO上一个动点.
如图,在平面直角坐标系中,动点A从原点O出发沿y轴正半轴以每秒1单位长度运动,运动的时间为t秒,过点A作x轴的平行线,交函数y=-$\frac{2}{x}$(x<0)的图象于B,交函数y=$\frac{6}{x}$(x>0)的图象于C,作射线BO,点D是射线BO上一个动点.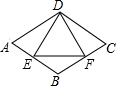 如图所示,菱形ABCD的周长为16cm,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为E,F,则△DEF的周长为6$\sqrt{3}$cm.
如图所示,菱形ABCD的周长为16cm,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为E,F,则△DEF的周长为6$\sqrt{3}$cm.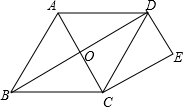 如图,O是菱形ABCD的对角线的交点,BC=2OC=2,DE=1,DE∥AC,
如图,O是菱形ABCD的对角线的交点,BC=2OC=2,DE=1,DE∥AC,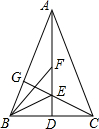 如图,△ABC中,AB=AC,AD⊥BC于点D,射线BE、BF将∠ABC三等分交AD于E、F两点,连接CE并延长交AB于点G,求证:$\frac{AF}{EF}$=$\frac{AG}{GB}$.
如图,△ABC中,AB=AC,AD⊥BC于点D,射线BE、BF将∠ABC三等分交AD于E、F两点,连接CE并延长交AB于点G,求证:$\frac{AF}{EF}$=$\frac{AG}{GB}$.