题目内容
6. 如图,在?ABCD中,∠DAB的角平分线交边CD于点E,AD=3,EC=2,则?ABCD的周长为16.
如图,在?ABCD中,∠DAB的角平分线交边CD于点E,AD=3,EC=2,则?ABCD的周长为16.
分析 由平行四边形ABCD得到AB=CD,AD=BC,DC∥AB,再和已知AE平分∠DAB,进一步推出∠DAE=∠EAB,即AD=DE,即可求出AB、AD的长,就能求出答案.
解答 解:
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,DC∥AB,
∴∠DEA=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠DAE=∠DEA,
∴AD=ED=3,
∵EC=2,
∴AB=DC=2+3=5
∴平行四边形的周长是2(AD+AB)=16.
故答案为:16.
点评 本题主要考查了平行四边形的性质,三角形的角平分线,平行线的性质,等腰三角形的判定等知识点,解此题的关键是综合运用性质进行证明.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
17.如图,是一组按照某种规律摆放成的图案,则图10中三角形的个数是( )


| A. | 100 | B. | 66 | C. | 36 | D. | 32 |
18. 如图,△ABC中,∠C=90°,AC=3cm,点P是边BC上的动点,则AP长不可能是( )
如图,△ABC中,∠C=90°,AC=3cm,点P是边BC上的动点,则AP长不可能是( )
 如图,△ABC中,∠C=90°,AC=3cm,点P是边BC上的动点,则AP长不可能是( )
如图,△ABC中,∠C=90°,AC=3cm,点P是边BC上的动点,则AP长不可能是( )| A. | 2.5cm | B. | 3cm | C. | 4cm | D. | 5cm |
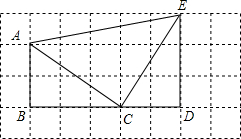 如图,若每个小方格边长为1,请你根据所学的知识判断△ACE是什么形状?并说明理由.
如图,若每个小方格边长为1,请你根据所学的知识判断△ACE是什么形状?并说明理由. 如图,∠A=30°,∠B=45°,∠C=40°,∠DFE=115°.
如图,∠A=30°,∠B=45°,∠C=40°,∠DFE=115°.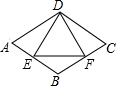 如图所示,菱形ABCD的周长为16cm,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为E,F,则△DEF的周长为6$\sqrt{3}$cm.
如图所示,菱形ABCD的周长为16cm,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为E,F,则△DEF的周长为6$\sqrt{3}$cm.