题目内容
6.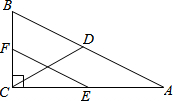 如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是AB、AC、BC的中点,若CD=10,则EF的长为( )
如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是AB、AC、BC的中点,若CD=10,则EF的长为( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
分析 根据直角三角形的性质求出AB的长,根据三角形中位线定理计算即可.
解答 解:∵∠ACB=90°,点D是AB的中点,
∴AB=2CD=20,
∵点E、F分别是AC、BC的中点,
∴EF=$\frac{1}{2}$AB=10,
故选:A.
点评 本题考查的是三角形中位线定理,三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
17. 某街道口五分钟内各种机动车(A:拖拉机;B:客车;C:货车;D:汽车)通过的车辆数如图所示,则下列说法不正确的是( )
某街道口五分钟内各种机动车(A:拖拉机;B:客车;C:货车;D:汽车)通过的车辆数如图所示,则下列说法不正确的是( )
 某街道口五分钟内各种机动车(A:拖拉机;B:客车;C:货车;D:汽车)通过的车辆数如图所示,则下列说法不正确的是( )
某街道口五分钟内各种机动车(A:拖拉机;B:客车;C:货车;D:汽车)通过的车辆数如图所示,则下列说法不正确的是( )| A. | 该街道口这五分钟内共通过150辆车 | |
| B. | 这五分钟内通过的货车车辆占总车辆数的20% | |
| C. | 该街道口这五分钟内通过的汽车车辆数最多 | |
| D. | 该街道口这五分钟内通过的货车车辆数最少 |
14. 如图所示,直线a,b被直线c,d所截,若∠1=∠2,∠3=114°,则∠4的度数为( )
如图所示,直线a,b被直线c,d所截,若∠1=∠2,∠3=114°,则∠4的度数为( )
 如图所示,直线a,b被直线c,d所截,若∠1=∠2,∠3=114°,则∠4的度数为( )
如图所示,直线a,b被直线c,d所截,若∠1=∠2,∠3=114°,则∠4的度数为( )| A. | 56° | B. | 60° | C. | 66° | D. | 76° |
1. 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要( )米.
如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要( )米.
 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要( )米.
如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要( )米.| A. | 5 | B. | 7 | C. | 8 | D. | 12 |
11.若a是有理数,则下列各式一定成立的有( )
| A. | -a2+1是负数 | B. | -(a+1)2是负数 | C. | a2+1是正数 | D. | |a-1|是正数 |
18.下列时刻中,分针与时针互相垂直的是( )
| A. | 2点20分 | B. | 6点25分 | C. | 12点10分 | D. | 9点整 |
15.下列方程无解的是( )
| A. | x2+3=2x2-1 | B. | (x-2)2=0 | C. | (2x+3)2=(1-x)2 | D. | x2+9=0 |
16. 如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=6,CD=2,则⊙O的半径为( )
如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=6,CD=2,则⊙O的半径为( )
 如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=6,CD=2,则⊙O的半径为( )
如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=6,CD=2,则⊙O的半径为( )| A. | 5 | B. | $\frac{5}{4}$ | C. | $\frac{13}{4}$ | D. | 4 |
 如图,A,B,C,D是⊙O上的四点,AB=CD,求证:AC=BD.
如图,A,B,C,D是⊙O上的四点,AB=CD,求证:AC=BD.