题目内容
14. 如图,A,B,C,D是⊙O上的四点,AB=CD,求证:AC=BD.
如图,A,B,C,D是⊙O上的四点,AB=CD,求证:AC=BD.
分析 根据圆心角、弧、弦的关系由AB=CD得到$\widehat{AB}$=$\widehat{CD}$,则$\widehat{BD}$=$\widehat{AC}$,所以AC=BD.
解答 证明:∵AB=CD,
∴$\widehat{AB}$=$\widehat{CD}$,
∴$\widehat{AB}$+$\widehat{AD}$=$\widehat{AD}$+$\widehat{CD}$,即$\widehat{BD}$=$\widehat{AC}$,
∴AC=BD.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
相关题目
4.如表是某校八年级(1)班20名学生某次数学测验的成绩统计表.
若这20名学生成绩的平均分数为82分,求x和y的值.
| 成绩(分) | 60 | 70 | 80 | 90 | 100 |
| 人数(人) | 1 | 5 | x | y | 2 |
8. 如图是一个长为4,宽为3,高为12矩形牛奶盒,从上底一角的小圆孔插入一根到达底部的直吸管,吸管在盒内部分a的长度范围是(牛奶盒的厚度、小圆孔的大小及吸管的粗细均忽略不计)( )
如图是一个长为4,宽为3,高为12矩形牛奶盒,从上底一角的小圆孔插入一根到达底部的直吸管,吸管在盒内部分a的长度范围是(牛奶盒的厚度、小圆孔的大小及吸管的粗细均忽略不计)( )
 如图是一个长为4,宽为3,高为12矩形牛奶盒,从上底一角的小圆孔插入一根到达底部的直吸管,吸管在盒内部分a的长度范围是(牛奶盒的厚度、小圆孔的大小及吸管的粗细均忽略不计)( )
如图是一个长为4,宽为3,高为12矩形牛奶盒,从上底一角的小圆孔插入一根到达底部的直吸管,吸管在盒内部分a的长度范围是(牛奶盒的厚度、小圆孔的大小及吸管的粗细均忽略不计)( )| A. | 5≤a≤12 | B. | 12≤a≤3$\sqrt{17}$ | C. | 12≤a≤4$\sqrt{10}$ | D. | 12≤a≤13 |
5.下列三边的长不能成为直角三角形三边的是( )
| A. | 3,4,5 | B. | 5,12,13 | C. | 4,5,6 | D. | 8,15,17 |
 如图,在2×4的正方形方格中,有格点△ABC(我们把顶点在正方形的顶点上的三角形叫做格点三角形),则与△ABC相似但不全等的格点三角形共有( )
如图,在2×4的正方形方格中,有格点△ABC(我们把顶点在正方形的顶点上的三角形叫做格点三角形),则与△ABC相似但不全等的格点三角形共有( ) 如图,在矩形ABCD中截取正方形ABMN,已知MN是BC和CM的比例中项,CM=3-$\sqrt{5}$,求AD的长.
如图,在矩形ABCD中截取正方形ABMN,已知MN是BC和CM的比例中项,CM=3-$\sqrt{5}$,求AD的长.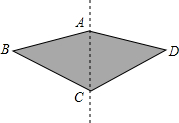 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°.求∠C的度数.
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°.求∠C的度数.
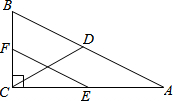 如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是AB、AC、BC的中点,若CD=10,则EF的长为( )
如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是AB、AC、BC的中点,若CD=10,则EF的长为( )