题目内容
1. 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要( )米.
如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要( )米.| A. | 5 | B. | 7 | C. | 8 | D. | 12 |
分析 当地毯铺满楼梯时其长度的和应该是楼梯的水平宽度与垂直高度的和,根据勾股定理求得水平宽度,然后求得地毯的长度即可.
解答 解:由勾股定理得:
楼梯的水平宽度=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
地毯的长度至少是3+4=7米.
故选B.
点评 此题考查了勾股定理的应用及平移的知识,属于基础题,利用勾股定理求出水平边的长度是解答本题的关键.

练习册系列答案
相关题目
12. 如图,O是直线AB上一点,若∠1=26°,则∠AOC为( )
如图,O是直线AB上一点,若∠1=26°,则∠AOC为( )
 如图,O是直线AB上一点,若∠1=26°,则∠AOC为( )
如图,O是直线AB上一点,若∠1=26°,则∠AOC为( )| A. | 154° | B. | 144° | C. | 116° | D. | 26°或154° |
9.桌面上摆着一些相同的小正方体木块,从正南方向看如图a,从正西方向看如图b,那么桌面上至少有这样的小正方体木块( )


| A. | 20块 | B. | 16块 | C. | 10块 | D. | 6块 |
16.如果有理数a、b、c的积是负号,则以下几种说法中,正确的是( )
| A. | 必有a<0,b<0,c<0 | |
| B. | 必有a<0,b>0,c>0 | |
| C. | 必有a>0,b<0,c<0 | |
| D. | 其中两个数大于零,一个数小于零或三个数都小于零 |
13.$\frac{a}{|a|}+\frac{b}{{|{-b}|}}$的所有可能的值有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10. 如图,用尺规作图法分别作出射线AE、BF,AE与BF交于点C,若AB=3,则AC的长为( )
如图,用尺规作图法分别作出射线AE、BF,AE与BF交于点C,若AB=3,则AC的长为( )
 如图,用尺规作图法分别作出射线AE、BF,AE与BF交于点C,若AB=3,则AC的长为( )
如图,用尺规作图法分别作出射线AE、BF,AE与BF交于点C,若AB=3,则AC的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 无法确定 |
11.已知x+y=6,x-y=1,则x2-y2等于( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
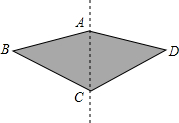 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°.求∠C的度数.
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°.求∠C的度数.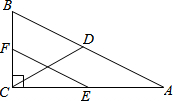 如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是AB、AC、BC的中点,若CD=10,则EF的长为( )
如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是AB、AC、BC的中点,若CD=10,则EF的长为( )