题目内容
16. 如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=6,CD=2,则⊙O的半径为( )
如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=6,CD=2,则⊙O的半径为( )| A. | 5 | B. | $\frac{5}{4}$ | C. | $\frac{13}{4}$ | D. | 4 |
分析 连结OA,如图,设⊙O的半径为r,根据垂径定理得到AC=BC=$\frac{1}{2}$AB=3,再在Rt△OAC中利用勾股定理得到(r-2)2+32=r2,然后解方程求出r即可.
解答  解:连结OA,如图,设⊙O的半径为r,
解:连结OA,如图,设⊙O的半径为r,
∵OD⊥AB,
∴AC=BC=$\frac{1}{2}$AB=8,
在Rt△OAC中,
∵OA=r,OC=OD-CD=r-2,AC=3,
∴(r-2)2+32=r2,解得r=$\frac{13}{4}$.
故选C.
点评 本题考查了的是垂径定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
7.为紧急安置60名地震中的灾民,需要同时搭建可容纳6人和4人的两种帐篷,正好安置完所有人且不多余,则搭建方案共有( )
| A. | 3种 | B. | 4种 | C. | 5种 | D. | 6种 |
4.有一块长为a,宽为b的长方形铝片,四角各截去一个相同的边长为x的正方形,折起来做成一个无盖的盒子,则此盒子的底面积应为( )
| A. | x2 | B. | (x-a)(b-x) | C. | ab | D. | (a-2x)(b-2x) |
11.已知x+y=6,x-y=1,则x2-y2等于( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
1.甲、乙、丙三位同学测一张长1.2m的办公桌,甲、乙均用分度值为1cm的刻度尺,丙用分度值为1mm的刻度尺,甲、乙、丙三人测出的数据分别为1.203m、12.0dm、120.1cm,其中正确的是( )
| A. | 三者都对 | B. | 甲对 | C. | 乙对 | D. | 丙对 |
8.有下面4个数:8、5、11、x,它们的最大值与最小值的差为10,则x的值为( )
| A. | 6 | B. | 1 | C. | 15 | D. | 1或15 |
6.平行四边形的两邻边分别为6和8,那么其对角线应( )
| A. | 大于2 | B. | 小于14 | C. | 大于2且小于14 | D. | 大于2或小于12 |
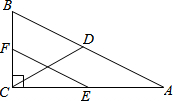 如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是AB、AC、BC的中点,若CD=10,则EF的长为( )
如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是AB、AC、BC的中点,若CD=10,则EF的长为( )