题目内容
18.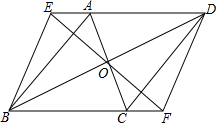 已知:如图,?ABCD中,对角线AC、BD交于点O,直线EF经过点O,分别交DA,BC的延长线于点E,F,连接BE,DF.
已知:如图,?ABCD中,对角线AC、BD交于点O,直线EF经过点O,分别交DA,BC的延长线于点E,F,连接BE,DF.求证:(1)AE=CF;
(2)四边形BEDF是平行四边形.
分析 (1)只要证明△AOE≌△COF即可;
(2)只要证明DE=BF,DE∥BF即可;
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠AEO=∠CFO,
∵∠AOE=∠COF,
∴△AOE≌△COF,
∴AE=CF;
(2)∵四边形ABCD是平行四边形,
∴AD=BC,
∵AE=CF,
∴AD+AE=BC+CF,
∴DE=BF,
∵DE∥BF,
∴四边形BEDF是平行四边形.
点评 本题考查平行四边形的判定和性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
9.已知方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$,那么方程组$\left\{\begin{array}{l}{{a}_{1}(x-1)+{b}_{1}(y+2)={c}_{1}}\\{{a}_{2}(x-1)+{b}_{2}(y+2)={c}_{2}}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=-5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=-5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ |
6.已知关于x的一元二次方程x2+x+m2-1=0的一个根是0,则m的值为( )
| A. | 1 | B. | 0 | C. | ?1 | D. | 1或?1 |
3. 如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )
如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )
 如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )
如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )| A. | AB=CD | B. | AD∥BC | C. | OA=OC | D. | AD=BC |
7.在某次救灾过程中,需要向A、B两个机场分别运送100吨和70吨生活物资,已知该物资在甲仓库存有90吨,乙仓库存有80吨,若从甲、乙两仓库运动物资到机场的费用(元/吨)如表所示:
(1)设从甲仓库运送到A机场的物资为x吨,求总运费y(元)与x(吨)之间的函数关系式,并写出x的取值范围;
(2)请设计并说明总运费最低时的调配方案,并求出这时的最低费用.
| 机场 | 运费(元/吨) | |
| 甲库 | 乙库 | |
| A机场 | 15 | 20 |
| B机场 | 10 | 8 |
(2)请设计并说明总运费最低时的调配方案,并求出这时的最低费用.
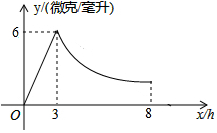 某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(时)之间的函数关系如图所示,当血液中药物浓度上升时,y与x成正比,下降时,y与x成反比.
某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(时)之间的函数关系如图所示,当血液中药物浓度上升时,y与x成正比,下降时,y与x成反比.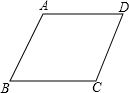 如图,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形,则应添加的一个条件是AD=BC(或AB∥CD或∠A=∠C或∠B=∠D).
如图,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形,则应添加的一个条件是AD=BC(或AB∥CD或∠A=∠C或∠B=∠D).