题目内容
8．$\left\{\begin{array}{l}{x-y=40，①}\\{x+\frac{1}{4}y=5．②}\end{array}\right.$解：原方程化为$\left\{\begin{array}{l}{x-y=40①}\\{4x+y=20②}\end{array}\right.$．
分析 把方程②的未知数的系数化为整数即可．
解答 解：原方程组化为$\left\{\begin{array}{l}{x-y=40①}\\{4x+y=20②}\end{array}\right.$，
故答案为：$\left\{\begin{array}{l}{x-y=40①}\\{4x+y=20②}\end{array}\right.$．
点评 本题考查了解二元一次方程组，熟练掌握二元一次方程组的解法是解题的关键．
练习册系列答案
相关题目
12．在平面直角坐标系中，点（-3，-x2-1）所在的象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
13．a6÷a3÷a4等于（ ）
| A． | a${\;}^{\frac{1}{2}}$ | B． | a-1 | C． | a-2 | D． | a13 |
10．下列运动属于平移的是（ ）
| A． | 冷水加热过程中小气泡上升成为大气泡 | |
| B． | 投篮时的篮球运动 | |
| C． | 急刹车时汽车在地面上的滑动 | |
| D． | 随风飘动的树叶在空中的运动 |
3．二次函数y=ax2+bx+c（a≠0）中，若当x取x1，x2（x1≠x2）时，函数值相等，则当x取x1+x2时，函数值等于（ ）
| A． | -$\frac{b}{2a}$ | B． | $\frac{b}{2a}$ | C． | $\frac{4ac-{b}^{2}}{4a}$ | D． | c |
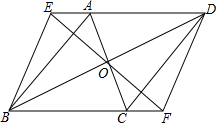已知：如图，?ABCD中，对角线AC、BD交于点O，直线EF经过点O，分别交DA，BC的延长线于点E，F，连接BE，DF．