Question

3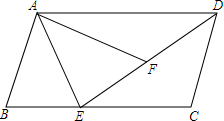．如图，在四边形ABCD中，AB=AF，AE是∠BAF的角平分线．
（1）求证：△ABE≌△AFE；
（2）若AB∥DC，求证：∠AFD=∠C．

Answer 1

分析 （1）根据AAS即可证明△ABE≌△AFE；
（2）根据全等三角形的性质和平行四边形的性质得到∠AFE=∠ADC，在由等式的性质即可得到∠FAD=∠CDE，然后根据三角形的内角和即可得到结论．

解答 证明：∵EA是∠BAF的角平分线，
∴∠BAE=∠FAE，
在△ABE和△AFE中，
$\left\{\begin{array}{l}{∠B=∠AFE}\\{∠BAE=∠FAE}\\{AE=AE}\end{array}\right.$，
∴△ABE≌△AFE；

（2）∵AB=CD，AB∥CD，
∴四边形ABCD是平行四边形，
∴∠B=∠ADC，
∵△ABE≌△AFE，
∴∠B=∠AFE，
∴∠AFE=∠ADC，
∵∠FAD=∠AFE-∠ADF，∠CDE=∠ADC-∠ADF，
∴∠FAD=∠CDE，
∵∠ADE=∠DEC，
∴∠AFD=180°-∠ADF-∠DAF，∠DCE=180°-∠DEC-∠EDC，
∴∠AFD=∠C．

点评 本题考查了平行四边形的判定与性质、全等三角形的判定与性质以及三角形内角和定理，熟练掌握平行四边形的判定与性质以及灵活运用三角形外角关系是解决问题的关键．