题目内容
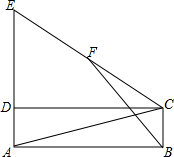 如图,在矩形ABCD中,延长AD至E,使AE=AC,F为CE的中点,连接BF.
如图,在矩形ABCD中,延长AD至E,使AE=AC,F为CE的中点,连接BF.(1)若AB=24,BC=7,求CE的长;
(2)求证:∠ACB=2∠CBF.
考点:全等三角形的判定与性质,直角三角形斜边上的中线,勾股定理
专题:
分析:(1)根据勾股定理可求AC的长,根据等量关系和线段之间的和差关系得到DE的长,再根据勾股定理可求CE的长;
(2)连结AF,过F点作FG⊥AB于G,根据等腰三角形三线合一的性质,以及四点共圆的性质即可求解.
(2)连结AF,过F点作FG⊥AB于G,根据等腰三角形三线合一的性质,以及四点共圆的性质即可求解.
解答:
 (1)解:在Rt△ABC中,∵AB=24,BC=7,
(1)解:在Rt△ABC中,∵AB=24,BC=7,
∴AC=
=25,
∵AE=AC,
∴AE=25,
∴DE=AE-AD=18,
在Rt△CDE中,CE=
=30,;
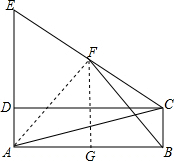
(2)证明:连结AF,过F点作FG⊥AB于G,
∵AE=AC,F为CE的中点,
∴AF⊥CE,
∴FG是等腰三角形AFB的角平分线,中线,
∴FG∥BC,
∴∠GFB=∠CBF,
∴∠AFB=2∠CBF,
∵∠AFC+∠ABC=90°+90°=180°,
∴A、B、C、F四点共圆,
∴∠ACB=∠AFB=2∠CBF.
 (1)解:在Rt△ABC中,∵AB=24,BC=7,
(1)解:在Rt△ABC中,∵AB=24,BC=7,∴AC=
| AB2+BC2 |
∵AE=AC,
∴AE=25,
∴DE=AE-AD=18,
在Rt△CDE中,CE=
| DE2+CD2 |
(2)证明:连结AF,过F点作FG⊥AB于G,
∵AE=AC,F为CE的中点,
∴AF⊥CE,
∴FG是等腰三角形AFB的角平分线,中线,
∴FG∥BC,
∴∠GFB=∠CBF,
∴∠AFB=2∠CBF,
∵∠AFC+∠ABC=90°+90°=180°,
∴A、B、C、F四点共圆,
∴∠ACB=∠AFB=2∠CBF.
点评:考查了勾股定理,等量关系和线段之间的和差关系,等腰三角形三线合一的性质,以及四点共圆的判定和性质,综合性较强,有一定的难度,解题的关键是根据题意作出辅助线.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
把(-2)2014+(-2)2015分解因式的结果是( )
| A、22015 |
| B、-22015 |
| C、-22014 |
| D、22014 |
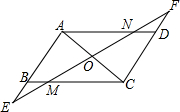 如图,已知:AB=DC,AD=BC.
如图,已知:AB=DC,AD=BC.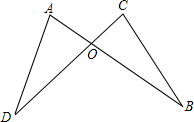 已知,如图,AB,CD相交于点O,且AB=CD,AD=CB.试说明OB=OD.
已知,如图,AB,CD相交于点O,且AB=CD,AD=CB.试说明OB=OD.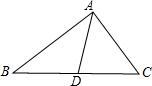 如图所示,在△ABC中,AB>AC,AD是△ABC的角平分线,请比较AB-AC与BD-DC的大小,并说明理由.
如图所示,在△ABC中,AB>AC,AD是△ABC的角平分线,请比较AB-AC与BD-DC的大小,并说明理由.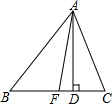 如图,在△ABC中,AD,AE分别是BC边上的高和中线,AB=7cm,AC=4cm,BC=6cm,求DE的长.
如图,在△ABC中,AD,AE分别是BC边上的高和中线,AB=7cm,AC=4cm,BC=6cm,求DE的长.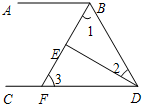 如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.