题目内容
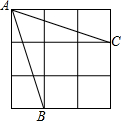 如图是一个3×3的正方形网格,那么tan∠BAC=
如图是一个3×3的正方形网格,那么tan∠BAC=考点:勾股定理,解直角三角形
专题:网格型
分析:连接BC,AD,可得AD⊥BC,根据勾股定理得到AB=AC,利用三线合一得到AD为角平分线,得到∠BAC=2∠BAD,利用锐角三角函数定义求出tan∠BAD值,再利用二倍角的正切函数公式求出tan∠BAC的值即可.
解答:
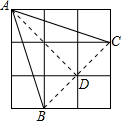 解:连接BC,AD,可得AD⊥BC,
解:连接BC,AD,可得AD⊥BC,
∵AB=AC=
=
,
∴AD平分∠BAC,
∴∠BAD=∠CAD=
∠BAC,
在Rt△ABD中,BD=
,AD=2
,
∴tan∠BAD=
,
则tan∠BAC=tan2∠BAD=
=
=
,
故答案为:
 解:连接BC,AD,可得AD⊥BC,
解:连接BC,AD,可得AD⊥BC,∵AB=AC=
| 12+32 |
| 10 |
∴AD平分∠BAC,
∴∠BAD=∠CAD=
| 1 |
| 2 |
在Rt△ABD中,BD=
| 2 |
| 2 |
∴tan∠BAD=
| 1 |
| 2 |
则tan∠BAC=tan2∠BAD=
| 2tan∠BAD |
| 1-tan2∠BAD |
2×
| ||
1-
|
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:此题考查了勾股定理,锐角三角函数定义,以及二倍角的正切函数公式,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、x+y是一次单项式 | ||||
B、多项式3
| ||||
| C、x的系数和次数都是1 | ||||
| D、单项式4×104x2的系数是4 |
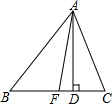 如图,在△ABC中,AD,AE分别是BC边上的高和中线,AB=7cm,AC=4cm,BC=6cm,求DE的长.
如图,在△ABC中,AD,AE分别是BC边上的高和中线,AB=7cm,AC=4cm,BC=6cm,求DE的长.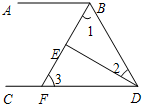 如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.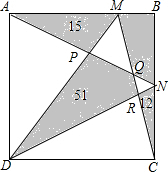 如图所示,ABCD是一个正方形,其中几块阴影部分的面积如图所示,则四边形BMQN的面积为
如图所示,ABCD是一个正方形,其中几块阴影部分的面积如图所示,则四边形BMQN的面积为 如图,正方形ABFG与正方形BCDE的面积之和为7,AD2-CG2=3,求AC•EF的值.
如图,正方形ABFG与正方形BCDE的面积之和为7,AD2-CG2=3,求AC•EF的值. 如图,在这个漂亮的螺旋图中,所有的三角形都是直角三角形,已知直角三角形有如下性质:直角三角形两直角边的平方和等于斜边的平方,如图中有结论OA2+AB2=OB2,OB2+BC2=OC2等.根据图中所标数据,试求出x,y,z,w的值,并指出其中的无理数.
如图,在这个漂亮的螺旋图中,所有的三角形都是直角三角形,已知直角三角形有如下性质:直角三角形两直角边的平方和等于斜边的平方,如图中有结论OA2+AB2=OB2,OB2+BC2=OC2等.根据图中所标数据,试求出x,y,z,w的值,并指出其中的无理数.