题目内容
17.商场销售某种小电器,每台进价为250元,市场调研表明:当售价为290元时,平均每天能售出30台;而当销售价每降低2元时,平均每天就能多售出6台,要想使这种小电器的销售利润平均每天达到1800元,求每台小电器应降价多少元?分析 销售利润=利润×销售数量,一台的利润=售价-进价,降低售价的同时,销售量就会提高,“一减一加”,根据每台的盈利×销售的件数=1800元,即可列方程求解.
解答 解:设每台小电器降价x元,根据题意,得
$(290-250-x)(30+6×\frac{x}{2})=1800$
解,得x1=10,x2=20
答:每台小电器降价10元或20元.
点评 此题主要考查了一元二次方程的应用,本题关键是会表示一台的利润,销售量增加的部分.找到关键描述语,找到等量关系:每台的盈利×销售的件数=1800元是解决问题的关键.

练习册系列答案
相关题目
9.6月30日以来的强降雨造成某地洪灾.某市组织20辆汽车装运食品、药品和生活用品三种物质共100吨前往灾区.按计划20辆汽车都要装运,且每辆汽车只能装运同一种物质,且必须装满.根据下表提供的信息,解答下列问题.
(1)设装运食品的车辆数为x,装运药品的车辆数为y,求y与x的函数关系式;
(2)如果装运食品的车辆数不少于5辆,装运药品的车辆数不少于4辆,那么有几种车辆安排方案?请写出所用的方案.
| 物资种类 | 食品 | 药品 | 生活用品 |
| 每辆汽车运载量(吨) | 6 | 5 | 4 |
(2)如果装运食品的车辆数不少于5辆,装运药品的车辆数不少于4辆,那么有几种车辆安排方案?请写出所用的方案.
6.下面图形中是中心对称但不是轴对称图形的是( )
| A. | 平行四边形 | B. | 长方形 | C. | 菱形 | D. | 正方形 |
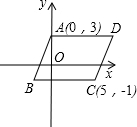 如图所示,在平面直角坐标系中,AD∥BC∥x轴,AD=BC=7,A(0,3),C(5,-1).
如图所示,在平面直角坐标系中,AD∥BC∥x轴,AD=BC=7,A(0,3),C(5,-1).