题目内容
已知抛物线过A(1,0)和B(4,0)两点,交y轴于C点,且BC=5,求该二次函数的解析式.
考点:待定系数法求二次函数解析式
专题:计算题
分析:由于已知抛物线与x轴的交点坐标,则可设交点式y=a(x-1)(x-4),再利用B点坐标和BC=5得到C点坐标,然后把C点坐标代入可求出a的值,从而得到两个解析式.
解答:解:设抛物线的解析式为y=a(x-1)(x-4),
∵B(4,0)两点,交y轴于C,BC=5,
∴C点坐标为(0,3)或(0,-3),
当C点坐标为(0,3),把(0,3)代入得a•(-1)•(-4)=3,解得a=
,
所以此时抛物线的解析式为y=
(x-1)(x-4)=-
x2-
x+5;
当C点坐标为(0,-5),把(0,-5)代入得a•(-1)•(-4)=-5,解得a=-
,
所以此时抛物线的解析式为y=-
(x-1)(x-4)=-
x2+
x-5,
所以该二次函数的解析式为y=-
x2-
x+5或y=-
x2+
x-5.
∵B(4,0)两点,交y轴于C,BC=5,
∴C点坐标为(0,3)或(0,-3),
当C点坐标为(0,3),把(0,3)代入得a•(-1)•(-4)=3,解得a=
| 3 |
| 4 |
所以此时抛物线的解析式为y=
| 3 |
| 4 |
| 3 |
| 4 |
| 15 |
| 4 |
当C点坐标为(0,-5),把(0,-5)代入得a•(-1)•(-4)=-5,解得a=-
| 3 |
| 4 |
所以此时抛物线的解析式为y=-
| 3 |
| 4 |
| 3 |
| 4 |
| 15 |
| 4 |
所以该二次函数的解析式为y=-
| 3 |
| 4 |
| 15 |
| 4 |
| 3 |
| 4 |
| 15 |
| 4 |
点评:本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
在日历上,如果某月的11日是星期四,那么这个月里下面哪个日期是星期五?( )
| A、4日 | B、19日 |
| C、20日 | D、30日 |
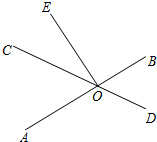 如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=30°,求∠AOD的度数.
如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=30°,求∠AOD的度数.