题目内容
已知等腰三角形内接于半径为5的圆O内,若底边BC的长为6,求AB的长.
考点:三角形的外接圆与外心,等腰三角形的性质,勾股定理,垂径定理
专题:
分析:连接AO并延长交BC于点D,连接OB,由垂径定理可得出BD的长,再根据勾股定理求出OD的长,进而可得出结论.
解答: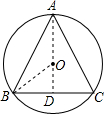 解:如图所示:
解:如图所示:
连接AO并延长交BC于点D,连接OB,
∵AB=AC,
∴AO⊥BC,
∵BC=6,
∴BD=3.
在Rt△OBD中,
∵OB=5,BD=3,
∴OD=
=
=4,
∴AD=AO+OD=5+4=9.
在Rt△ABD中,
∵BD=3,AD=9,
∴AB=
=
=3
.
同理,当该等腰三角形是钝角三角形时,AB=
.
综上所述,AB的长度是3
或
 解:如图所示:
解:如图所示:连接AO并延长交BC于点D,连接OB,
∵AB=AC,
∴AO⊥BC,
∵BC=6,
∴BD=3.
在Rt△OBD中,
∵OB=5,BD=3,
∴OD=
| OB2-BD2 |
| 52-32 |
∴AD=AO+OD=5+4=9.
在Rt△ABD中,
∵BD=3,AD=9,
∴AB=
| AD2+BD2 |
| 92+32 |
| 10 |
同理,当该等腰三角形是钝角三角形时,AB=
| 10 |
综上所述,AB的长度是3
| 10 |
| 10 |
点评:本题考查的是三角形的外接圆与外心,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
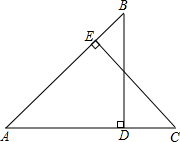 如图,BD⊥AC,CE⊥AB,垂足分别为D、E,AD=AE.下列方法中,可以直接判断△ADB≌△AEC的是( )
如图,BD⊥AC,CE⊥AB,垂足分别为D、E,AD=AE.下列方法中,可以直接判断△ADB≌△AEC的是( )| A、SSS | B、SAS |
| C、ASA | D、AAS |
 已知,在△ABC中,DE∥BC,F是AB上一点,FE的延长线交BC的延长线于点G,则∠EGH与∠ADE的大小有什么关系?请说明理由.
已知,在△ABC中,DE∥BC,F是AB上一点,FE的延长线交BC的延长线于点G,则∠EGH与∠ADE的大小有什么关系?请说明理由.