题目内容
在Rt△ABC中,斜边AB=2
,且tanA+tanB=
,求Rt△ABC的面积.
| 2 |
| ||
| 2 |
考点:解直角三角形,勾股定理
专题:
分析:根据锐角三角函数的定义:tanA=
,tanB=
,代入tanA+tanB=
,再根据勾股定理可求出两直角边或其乘积,代入直角三角形面积公式s=
ab求解.
| a |
| b |
| b |
| a |
| ||
| 2 |
| 1 |
| 2 |
解答:解:∵在Rt△ABC中,斜边AB=2
,
∴tanA=
,tanB=
,tanA+tanB=
,
∴
+
=
,
即:
=
.
由勾股定理得:a2+b2=(a+b)2-2ab=(2
)2,
∴ab=8
.
因此S△ABC=
ab=4
.
| 2 |
∴tanA=
| a |
| b |
| b |
| a |
| ||
| 2 |
∴
| a |
| b |
| b |
| a |
| ||
| 2 |
即:
| a2+b2 |
| ab |
| ||
| 2 |
由勾股定理得:a2+b2=(a+b)2-2ab=(2
| 2 |
∴ab=8
| 2 |
因此S△ABC=
| 1 |
| 2 |
| 2 |
点评:本题主要考查解直角三角形,勾股定理和三角函数的定义,难度适中.

练习册系列答案
相关题目
在△ABC中,BD、CF分别是AC、AB边上的中线,且BD=CF,则△ABC是( )
| A、不等边三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、直角三角形 |
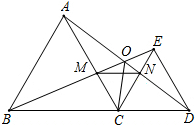 如图,已知△ABC和△CDE都是等边三角形,点B、C、D在同一条直线上,BE交AC于M,AD交CE于N,AD、BE交点O.求证:
如图,已知△ABC和△CDE都是等边三角形,点B、C、D在同一条直线上,BE交AC于M,AD交CE于N,AD、BE交点O.求证: