题目内容

1．在?ABCD中，对角线AC与BD相交于点O，AO+BO=6，则AC+BD等于（　　）
A．6B．12C．16D．18

分析 根据平行四边形的对角线互相平分即可求解．

解答 解：∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
∴AC=2AO，BD=2BO，
∴AC+BD=2（AO+BO）=12，
故选B．

点评 本题考查的是平行四边形的对角线互相平分这一性质，题型简单，解题的关键是熟记平行四边形的各种性质．

练习册系列答案
相关题目
12．如图，菱形ABCD的周长为16，∠ABC=120°，则AC的长为（　　）
A．4$\sqrt{3}$B．4C．2$\sqrt{3}$D．2
12．已知：如图，△CBE是一个锐角三角形，分别以CB，CE为边向外侧作等边三角形ABC和等边三角形CDE，连接AE、BD．
（1）求证：△ACE≌△BCD；
（2）若点P是边BE上的一个动点（不与两端点B、E重合），过点P作PM∥AE交AB于M，PN∥BD交DE于N．
①当点P是BE的中点时，求证：PM+PN=AE；
②当点P是BE上任意一点时，请问PM、PN、AE是否还有①中的结论，若有请说明理由；若没有则这三条线段有怎样的数量关系并说明理由？
9．如果直线y=3x+6与y=2x-4交点坐标为（a，b），则解为$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$的方程组是（　　）
A．$\left\{\begin{array}{l}{y-3x=6}\\{2y+x=-4}\end{array}\right.$B．$\left\{\begin{array}{l}{y-3x=6}\\{2y-x=4}\end{array}\right.$C．$\left\{\begin{array}{l}{3x-y=6}\\{3x-y=4}\end{array}\right.$D．$\left\{\begin{array}{l}{3x-y=-6}\\{2x-y=4}\end{array}\right.$
16．已知关于x，y的方程组$\left\{\begin{array}{l}{x+5y=4-a}\\{x-3y=3a}\end{array}\right.$，给出下列结论：
①$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$是方程组的解；
②当x=y时，a=-$\frac{1}{2}$；
③当a=-2时，x、y的值互为相反数
其中正确的是（　　）
A．0个B．1个C．2个D．3个
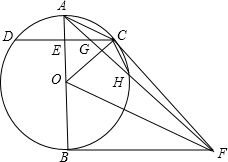6．如图，已知AB是⊙O的直径，C是⊙O上任一点（不与A，B重合），AB⊥CD于E，BF为⊙O的切线，OF∥AC，连结AF，FC，AF与CD交于点G，与⊙O交于点H，连结CH．
（1）求证：FC是⊙O的切线；
（2）求证：GC=GE；
（3）若cos∠AOC=$\frac{2}{3}$，⊙O的半径为r，求CH的长．
13．如图1，有若干张边长为a的小正方形①、长为b宽为a的长方形②以及边长为b的大正方形③的纸片．

（1）如果现有小正方形①1张，大正方形③2张，长方形②3张，请你将它们拼成一个大长方形 （在图2虚线框中画出图形），并运用面积之间的关系，将多项式a2+3ab+2b2分解因式．
（2）已知小正方形①与大正方形③的面积之和为169，长方形②的周长为34，求长方形②的面积．
（3）现有三种纸片各8张，从其中取出若干张纸片，每种纸片至少取一张，把取出的这些纸片拼成一个正方形（按原纸张进行无空隙、无重叠拼接），求可以拼成多少种边长不同的正方形．
10．若关于x的方程x2+px+q=0（p、q为常数）的两个实数根分别为2和-3，则p、q的值分别为（　　）
A．2，-3B．-1，-6C．1，-6D．1，6
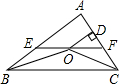11．如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB与E，交AC于F，过点O作OD⊥AC于D，下列四个结论：其中正确的结论是（　　）
①EF=BE+CF；
②∠BOC=90°+$\frac{1}{2}$∠A；
③设OD=m，AE+AF=n，则S△AEF=mn．
④EF不能成为△ABC的中位线．
A．1个B．2个C．3个D．4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网