题目内容
13.如图1,有若干张边长为a的小正方形①、长为b宽为a的长方形②以及边长为b的大正方形③的纸片.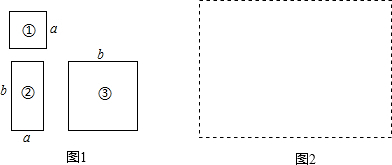
(1)如果现有小正方形①1张,大正方形③2张,长方形②3张,请你将它们拼成一个大长方形 (在图2虚线框中画出图形),并运用面积之间的关系,将多项式a2+3ab+2b2分解因式.
(2)已知小正方形①与大正方形③的面积之和为169,长方形②的周长为34,求长方形②的面积.
(3)现有三种纸片各8张,从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(按原纸张进行无空隙、无重叠拼接),求可以拼成多少种边长不同的正方形.
分析 (1)根据小正方形①1张,大正方形③2张,长方形②3张,直接画出图形,利用图形分解因式即可;
(2)由长方形②的周长为34,得出a+b=17,由题意可知:小正方形①与大正方形③的面积之和为a2+b2=169,将a+b=17两边同时平方,可求得ab的值,从而可求得长方形②的面积;
(3)设正方形的边长为(na+mb),其中(n、m为正整数)由完全平方公式可知:(na+mb)2=n2a2+2nmab+m2b2.因为现有三种纸片各8张,
n2≤8,m2≤8,2mn≤8(n、m为正整数)从而可知n≤2,m≤2,从而可得出答案.
解答 解:(1)如图: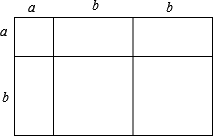
拼成边为(a+2b)和(a+b)的长方形
∴a2+3ab+2b2=(a+2b)(a+b);
(2)∵长方形②的周长为34,
∴a+b=17.
∵小正方形①与大正方形③的面积之和为169,
∴a2+b2=169.
将a+b=17两边同时平方得:(a+b)2=172,整理得:a2+2ab+b2=289,
∴2ab=289-169,
∴ab=60.
∴长方形②的面积为60.
(3)设正方形的边长为(na+mb),其中(n、m为正整数)
∴正方形的面积=(na+mb)2=n2a2+2nmab+m2b2.
∵现有三种纸片各8张,
∴n2≤8,m2≤8,2mn≤8(n、m为正整数)
∴n≤2,m≤2.
∴共有以下四种情况;
①n=1,m=1,正方形的边长为a+b;
②n=1,m=2,正方形的边长为a+2b;
③n=2,m=1,正方形的边长为2a+b;
④n=2,m=2,正方形的边长为2a+2b.
点评 此题考查因式分解的运用,要注意结合图形解决问题,解题的关键是灵活运用完全平方公式.

练习册系列答案
相关题目
1.在?ABCD中,对角线AC与BD相交于点O,AO+BO=6,则AC+BD等于( )
| A. | 6 | B. | 12 | C. | 16 | D. | 18 |
8.甲、乙两个工程队各自维修2800米的路面,甲工程队每小时维修路面的速度是乙工程队每小时维修路面速度的4倍,结果甲比乙早2小时完成了任务.设乙工程队每小时维修路面x米,则下面所列方程正确的是( )
| A. | $\frac{2800}{x}$-$\frac{2800}{5x}$=2 | B. | $\frac{2800}{5x}$-$\frac{2800}{x}$=2 | C. | $\frac{2800}{x}$-$\frac{2800}{4x}$=2 | D. | $\frac{2800}{4x}$-$\frac{2800}{x}$=2 |
 如图,长方形的长AD=9,宽AB=3,则图中阴影部分的面积为9.
如图,长方形的长AD=9,宽AB=3,则图中阴影部分的面积为9.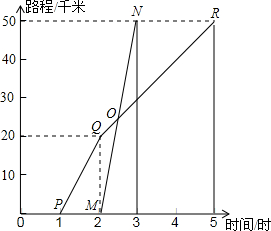 如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.
如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.