题目内容
1.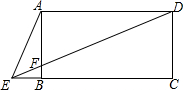 如图,四边形ABCD是矩形,点E为CB延长线上一点,DE交AB于F,且∠AED=2∠CED,若BE=1,AB=3,求DF的长.
如图,四边形ABCD是矩形,点E为CB延长线上一点,DE交AB于F,且∠AED=2∠CED,若BE=1,AB=3,求DF的长.
分析 取DF的中点G,连接AG,由矩形的性质得出∠BAD=∠ABC=∠ABE=90°,AD∥BC,得出∠ADE=∠CED,由勾股定理求出AE,证明∠AEG=∠AGE,得出AG=AE=$\sqrt{10}$,即可求出DF的长.
解答 解:取DF的中点G,连接AG,如图所示: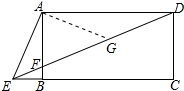
∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠ABE=90°,AD∥BC,
∴∠ADE=∠CED,
根据勾股定理得:AE=$\sqrt{B{E}^{2}+A{B}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∵G为DF的中点,
∴AG=DG=EG=$\frac{1}{2}$DF,
∴∠ADE=∠GAD,
∴∠AGE=∠GAD+∠ADG=2∠ADG,
∵∠AED=2∠CED,
∴∠AEG=∠AGE,
∴AG=AE=$\sqrt{10}$,
∴DF=2AG=2$\sqrt{10}$.
点评 本题考查了矩形的性质、勾股定理、直角三角形斜边上的中线性质、等腰三角形的判定;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
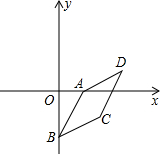 如图:在平面直角坐标系中,A(a,0),D(6,4),将线段AD平移到BC,使B(0,b),且a,b满足|2-a|+$\sqrt{6+b}$=0
如图:在平面直角坐标系中,A(a,0),D(6,4),将线段AD平移到BC,使B(0,b),且a,b满足|2-a|+$\sqrt{6+b}$=0