题目内容
16.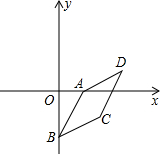 如图:在平面直角坐标系中,A(a,0),D(6,4),将线段AD平移到BC,使B(0,b),且a,b满足|2-a|+$\sqrt{6+b}$=0
如图:在平面直角坐标系中,A(a,0),D(6,4),将线段AD平移到BC,使B(0,b),且a,b满足|2-a|+$\sqrt{6+b}$=0(1)求A点、B点的坐标;
(2)设点M(-3,n)且三角形ABM的面积为16,求n的值;
(3)若∠DAO=150°,设点P是x轴上的一动点(不与点A重合),问∠APC与∠PCB存在什么具体的数量关系?写出你的证明结论并证明.
分析 (1)根据非负数的性质即可得到结果;
(2)根据勾股定理求得AB的长度,求出直线AB的解析式,然后根据点到直线的距离即可得到结果;
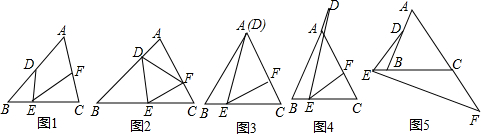
(3)分两种情况:①当点P在点A的右侧如图1,连接PC,延长BC交x轴于E,②当点P在点A的左侧如图2,连接PC,延长DA交PC于F,根据平移的性质和外角的性质即可得到结论.
解答 解:(1)∵a,b满足|2-a|+$\sqrt{6+b}$=0,
∴2-a=0,6+b=0,
∴a=2,b=-6,
∴A(2,0),B(0,-6);
(2)由(1)得A(2,0),B(0,-6),
∴OA=2,OB=6,
∴AB=$\sqrt{A{O}^{2}+O{B}^{2}}$=2$\sqrt{10}$,
∵三角形ABM的面积为16,
∴点M到直线AB的距离为:$\frac{8\sqrt{10}}{5}$,
∴直线AB的解析式为:y=3x-6,
根据点到直线的距离得:$\frac{|3×(-3)-n-6|}{\sqrt{{3}^{2}+(-1)^{2}}}$=$\frac{8\sqrt{10}}{5}$,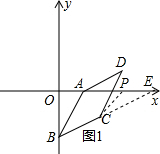
解得:n=1或n=-31;
(3)①当点P在点A的右侧如图1,连接PC,延长BC交x轴于E,
∵AD平移到BC,
∴AD∥BC,
∵∠DAO=150°,
∴∠DAE=30°,
∵∠AEC=30°,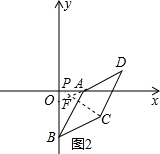
∴∠PCE=∠APC-30°,
∵∠PCB+∠PCE=∠PCB+∠APC-30°=180°,
∴∠PCB+∠APC=210°;
②当点P在点A的左侧如图2,连接PC,延长DA交PC于F,
∵∠DAO=150°,
∴∠PAF=30°,
∵AD∥BC,
∴∠AFC=∠PCB,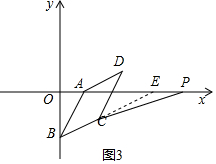
∵∠AFC=∠APC+30°,
∴∠PCB-∠APC=30°;
③当p在直线BC与x轴交点的右侧时,
∵∠DAO=150°,
∴∠DAP=30°,
∴∠OEC=30°,
∴∠ECP=30°-∠APC,
∴∠BCP=180°-∠ECP=150°+∠APC,
∴∠BCP-∠APC=150°.
点评 本题考查了坐标与图形的关系,平移的性质,三角形的面积,勾股定理,点到直线的距离公式,正确的画出图形是解题的关键.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案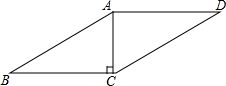 如图,在?ABCD中,过A点作高,垂足刚好为点C,AB=4,AC=2,则?ABCD的周长是( )
如图,在?ABCD中,过A点作高,垂足刚好为点C,AB=4,AC=2,则?ABCD的周长是( )| A. | 8+4$\sqrt{3}$ | B. | 4+2$\sqrt{3}$ | C. | 8 | D. | 4 |
| A. | 平均数 | B. | 极差 | C. | 中位数 | D. | 众数 |
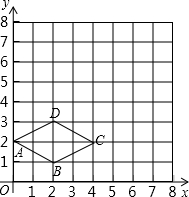 如图,在平面直角坐标系中,菱形ABCD各顶点均在格点上.
如图,在平面直角坐标系中,菱形ABCD各顶点均在格点上.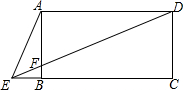 如图,四边形ABCD是矩形,点E为CB延长线上一点,DE交AB于F,且∠AED=2∠CED,若BE=1,AB=3,求DF的长.
如图,四边形ABCD是矩形,点E为CB延长线上一点,DE交AB于F,且∠AED=2∠CED,若BE=1,AB=3,求DF的长.