题目内容
16．若$\frac{x}{3}$=$\frac{y}{4}$=$\frac{z}{5}$，求$\frac{x-2y+3z}{x+2y-3z}$的值．分析 根据比例的性质，可用x表示y，用x表示z，根据分式的性质，可得答案．
解答 解：由$\frac{x}{3}$=$\frac{y}{4}$=$\frac{z}{5}$，得
y=$\frac{4x}{3}$，z=$\frac{5x}{3}$，
$\frac{x-2y+3z}{x+2y-3z}$=$\frac{x-2×\frac{4x}{3}+3×\frac{5x}{3}}{x+2×\frac{4x}{3}-3×\frac{5x}{3}}$=$\frac{\frac{10x}{3}}{-\frac{4x}{3}}$=-$\frac{5}{2}$．
点评 本题考查了比例的性质，利用比例的性质得出y=$\frac{4x}{3}$，z=$\frac{5x}{3}$是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
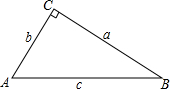如图，在△ABC中，∠C=90°，若a=2，b=1.5，则c=2.5；若a=7，c=25，则b=24；若a：b=3：4，c=15，则a=9，b=12．
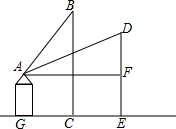起重机的吊杆与水平线夹角叫倾角，某起重机机身高20米，吊杆倾角是30°时，工作的水平距离AF为10$\sqrt{3}$米，求：当吊杆倾角是60°时，工作的高度BC．
如图，已知AB是⊙O的直径，C为AB延长线上的一点，CE交⊙O于点D，且CD=OA．求证：∠C=$\frac{1}{3}$∠AOE．
如图，△ABC≌△ADE，BA⊥AE，∠BAC=30°，求△ABD的度数．