题目内容
8. 如图,已知AB是⊙O的直径,C为AB延长线上的一点,CE交⊙O于点D,且CD=OA.求证:∠C=$\frac{1}{3}$∠AOE.
如图,已知AB是⊙O的直径,C为AB延长线上的一点,CE交⊙O于点D,且CD=OA.求证:∠C=$\frac{1}{3}$∠AOE.
分析 根据等腰三角形的性质,可得∠COD=∠C,∠CEO=∠ODE,根据三角形外角的性质,可得∠ODE=∠COD+∠C,∠AOE=∠C+∠CEO,根据等式的性质,可得答案.
解答 证明:如图:连接OD,
∵OD=OA,CD=OA
∴OD=CD,
∴∠COD=∠C.
∵∠ODE是△OCD的外角,
∴∠ODE=∠COD+∠C=2∠C.
∵OD=OE,
∴∠CEO=∠ODE=2∠C.
∵∠AOE是△OCE的外角,
∴∠AOE=∠C+∠CEO=3∠C
∴∠C=$\frac{1}{3}$∠AOE.
点评 本题考查了圆的认识,利用等腰三角形的性质,三角形外角的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 a、b、c的位置如图所示,化简|a+b|+|b+c|-|a-c|-|b-a|.
a、b、c的位置如图所示,化简|a+b|+|b+c|-|a-c|-|b-a|.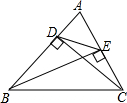 如图,CD,BE是△ABC的两条高,求证:△ABC∽△AED.
如图,CD,BE是△ABC的两条高,求证:△ABC∽△AED.