Question

4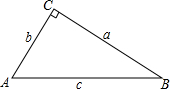．如图，在△ABC中，∠C=90°，若a=2，b=1.5，则c=2.5；若a=7，c=25，则b=24；若a：b=3：4，c=15，则a=9，b=12．

Answer 1

分析 在直角三角形ABC中，根据a与b的值，利用勾股定理求出c的值；根据a与c的值，利用勾股定理求出b的值；根据a与b的比值设出a与b，再由c的值，利用勾股定理求出a与b的值即可．

解答 解：在△ABC中，∠C=90°，a=2，b=1.5，
根据勾股定理得：c=$\sqrt{{2}^{2}+1．{5}^{2}}$=2.5；
若a=7，c=25，根据勾股定理得：b=$\sqrt{2{5}^{2}-{7}^{2}}$=24；
若a：b=3：4，c=15，设a=3k，b=4k，
根据勾股定理得：9k²+16k²=225，即k²=9，
解得：k=3（负值舍去），
则a=9，b=12，
故答案为：2.5；24；9；12

点评 此题考查了勾股定理，熟练掌握勾股定理是解本题的关键．