题目内容
16.函数y=$\frac{\sqrt{{x}^{2}-3x-4}}{x+1}$的自变量x的取值范围是x<-1或x≥4.分析 根据被开方数为非负数和分母不能为0计算即可.
解答 解:由题意得,x2-3x-4≥0,x+1≠0,
解得,x<-1或x≥4,
故答案为:x<-1或x≥4.
点评 本题考查的是函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数为非负数.

练习册系列答案
相关题目
1.已知3m2-2m-5=0,5n2+2n-3=0,其中m,n为实数,则|m-$\frac{1}{n}$|=( )
| A. | 0 | B. | $\frac{8}{3}$ | C. | $\frac{5}{3}$ | D. | 0或$\frac{8}{3}$ |
8.某珠宝店失窃,甲、乙、丙、丁四人涉嫌被拘审,四人的口供如下:甲:作案的是丙;乙:丁是作案者;丙:如果我作案,那么丁是主犯;丁:作案的不是我.如果四人口供中只有一个是假的,那么以下判断正确的是( )
| A. | 说假话的是甲,作案的是乙 | B. | 说假话的是丁,作案的是丙和丁 | ||
| C. | 假话的是乙,作案的是丙 | D. | 说假话的是丙,作案的是丙 |
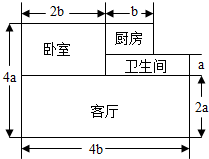 李叔叔买了一套新房,其结构如图(单位:m),他打算除卧室外,其余部分铺地砖.
李叔叔买了一套新房,其结构如图(单位:m),他打算除卧室外,其余部分铺地砖. 如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC,∠BAC=120°,BC=12cm,则DE=3cm.
如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC,∠BAC=120°,BC=12cm,则DE=3cm.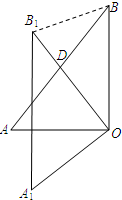 如图,△AOB中,∠AOB=90°,AO=6,BO=8,将△AOB绕顶点O逆时针旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,则线段BB1的长度为$\frac{8\sqrt{10}}{5}$.
如图,△AOB中,∠AOB=90°,AO=6,BO=8,将△AOB绕顶点O逆时针旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,则线段BB1的长度为$\frac{8\sqrt{10}}{5}$.